题目内容
某地球仪上北纬30°纬线长度为12πcm,该地球仪的表面上北纬30°东经30°对应点A与北纬30°东经90°对应点B之间的球面距离为 cm(精确到0.01).
考点:球面距离及相关计算
专题:计算题,空间位置关系与距离
分析:先求纬圆半径,再求地球仪的半径,A、B两地在同一纬度圈上,计算经度差,求出AB弦长,以及球心角,然后求出球面距离.
解答:
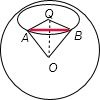 解:地球仪上北纬30°纬线的长度为12πcm,则纬圆半径r,2πr=12π
解:地球仪上北纬30°纬线的长度为12πcm,则纬圆半径r,2πr=12π
∴r=6,
∴地球仪的半径R=
=4
cm.
∵北纬30°东经30°对应点A与北纬30°东经90°对应点B,
∴北纬30°的纬圆半径是2
cm,经度差是60°,
∴AB=6cm,
设球心角为α,则cosα=
,
∴α=arccos
,
∴球面距离为l=αR=4
•arccos
=6.2053≈6.21cm.
故答案为:6.21.
 解:地球仪上北纬30°纬线的长度为12πcm,则纬圆半径r,2πr=12π
解:地球仪上北纬30°纬线的长度为12πcm,则纬圆半径r,2πr=12π∴r=6,
∴地球仪的半径R=
| r |
| cos30° |
| 3 |
∵北纬30°东经30°对应点A与北纬30°东经90°对应点B,
∴北纬30°的纬圆半径是2
| 3 |
∴AB=6cm,
设球心角为α,则cosα=
| 5 |
| 8 |
∴α=arccos
| 5 |
| 8 |
∴球面距离为l=αR=4
| 3 |
| 5 |
| 8 |
故答案为:6.21.
点评:本题考查球面距离及其他计算,考查空间想象能力,是基础题.

练习册系列答案
相关题目
按照如图的程序框图执行,若输出的X值为31,则M处的条件为( )


| A、k≤2 | B、k<3 |
| C、k≤3 | D、k≤4 |
如图所示的程序框图,如果输入m=225,n=135,那么输出的值为( )


| A、45 | B、5 | C、15 | D、90 |
 若F1、F2分别是椭圆
若F1、F2分别是椭圆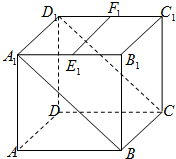 如图,A1B1C1D-ABCD为边长为a的正方体,E,F分别是A1B1,C1D的中点,过EF作正方体截面,若截面平行于平面A1BCD1,则截面的面积为
如图,A1B1C1D-ABCD为边长为a的正方体,E,F分别是A1B1,C1D的中点,过EF作正方体截面,若截面平行于平面A1BCD1,则截面的面积为