题目内容
5.函数f(x)=$\frac{sin4x}{1+cos4x}$的最小正周期是$\frac{π}{2}$.分析 利用三角函数公式化简只有一个函数名,即可求解周期.
解答 解:函数f(x)=$\frac{sin4x}{1+cos4x}$=$\frac{2sin2xcos2x}{1+cos2•2x}=\frac{2sin2xcos2x}{1+2co{s}^{2}2x-1}$=tan2x.
∴最小正周期T=$\frac{π}{2}$.
故答案为$\frac{π}{2}$.
点评 本题主要考查三角函数的化简能力及图象和性质,比较基础.

练习册系列答案
相关题目
15.若向量$\overrightarrow a=(3,2)$,$\overrightarrow b=(0,-1)$,则向量$\vec a+\vec b$的坐标是( )
| A. | (3,-1) | B. | (-3,1) | C. | (-3,-1) | D. | (3,1) |
16.若函数f(x)=x(x-c)2在x=3处有极大值,则c=( )
| A. | 9 | B. | 3 | C. | 3或9 | D. | 以上都不对 |
13.甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是
由此判断性能较好的一台是乙.
| 甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
20.在△ABC中,点D满足$\overrightarrow{BC}$=3$\overrightarrow{BD}$,则( )
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ |
17.运行如图所示的程序框图,若输入的n=3,x=2,则输出的y的值为( )


| A. | 9 | B. | 18 | C. | 20 | D. | 35 |
14.已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与(x-2)2+(y-4)2=9相外切,若过点P(-1,1)的直线l与圆C交于A,B两点,当∠ACB最小时,弦AB的长为( )
| A. | 4 | B. | $2\sqrt{3}$ | C. | 2 | D. | $\sqrt{3}$ |
15.已知函数f(x)=2x+x-4,g(x)=ex+x-4,h(x)=lnx+x-4的零点分别是a,b,c,则a,b,c的大小顺序是( )
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | c<a<b |
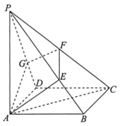 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处).
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA丄底面ABCD,PA=AC.过点A的平面与棱PB,PC,PD分别交于点E,F,G(E,F,G三点均不在棱的端点处).