题目内容
5.已知 函数f(x)=x3+(m-4)x2-3mx+(n-6)x∈R的图象关于原点对称,其中m,n为实常数.(1)求m,n的值;
(2)试用单调性的定义证明:f(x)在区间[-2,2]上是单调函数;
(3)当-2≤x≤2 时,不等式f(x)≥(n-logma)logma恒成立,求实数a的取值范围.
分析 (1)利用函数的对称性,得到方程,转化求解m,n即可.
(2)利用函数的单调性的定义直接证明即可.
(3)利用函数的单调性结合函数的定义域,转化求解即可.
解答 (本题14分)
解:(1)由已知得f(x)为奇函数∴f(-x)=-f(x)即-x3+(m-4)x2+3mx+(n-6)=-x3-(m-4)x2+3mx-(n-6)恒成立,即(m-4)x2+(n-6)=0恒成立,∴m=4,n=6…(4分)
(2)由(1)的f(x)=x3-12x,设-2≤x1<x2≤2,$f({x_1})-f({x_2})=x_1^3-12{x_1}-x_2^3+12x{\;}_2=({x_1}-{x_2})(x_1^2+{x_1}{x_2}+x_2^2-12)$,
∵-2≤x1<x2≤2,∴${x_1}-{x_2}<0,x_1^2+{x_1}{x_2}+x_2^2-12<0$,
∴f(x1)-f(x2)>0,
即∴f(x1)>f(x2),
∴f(x)在[-2,2]上是减函数 …(10分)
(3)由(2)知f(x)在[-2,2]上是减函数,
则f(x)≥f(2)=-16-16≥(6-log4a)log4a,
∴(log4a-8)(log4a+2)≥0,
∴log4a≤-2或log4a≥8,
∴$0<a≤\frac{1}{16}$或a≥48…(14分)
点评 本题考查函数的恒成立条件的应用,函数的单调性,考查转化思想以及计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
15.△ABC的内角A,B满足cosAcosB>sinAsinB,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等边三角形 |
10.二次函数y=x2+bx+c的图象的对称轴是x=2,则有( )
| A. | f(1)<f(2)<f(4) | B. | f(2)<f(1)<f(4) | C. | f(2)<f(4)<f(1) | D. | f(4)<f(2)<f(1) |
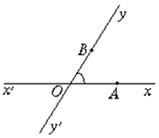 如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:
如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问: 为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行秋季校园足球联赛,为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,得到茎叶图如下:
为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行秋季校园足球联赛,为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,得到茎叶图如下: