题目内容
15.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1,F2,椭圆上一点M($\frac{2\sqrt{6}}{3},\frac{\sqrt{3}}{3}$),$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$=0,满足.则椭圆的方程是$\frac{{x}^{2}}{4}$+y2=1.分析 利用数量积运算性质、点与椭圆的位置关系转化为点的坐标满足椭圆方程即可得出.
解答 解:设F1(-c,0),F2(c,0),∴$\overrightarrow{M{F}_{1}}$=$(-c-\frac{2\sqrt{6}}{3},-\frac{\sqrt{3}}{3})$,$\overrightarrow{M{F}_{2}}$=$(c-\frac{2\sqrt{6}}{3},\frac{\sqrt{3}}{3})$.
∵$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$=0,∴$(\frac{2\sqrt{6}}{3})^{2}$-c2+$(\frac{\sqrt{3}}{3})^{2}$=0,
∴c2=3.
∴a2-b2=3,①
又点M在椭圆上,∴$\frac{8}{3{a}^{2}}$+$\frac{1}{3{b}^{2}}$=1 ②
由①代入②得:$\frac{8}{3{a}^{2}}$+$\frac{1}{3({a}^{2}-3)}$=1,
整理为:a4-6a2+8=0,
解得a2=2,或4,
∵a2>3,∴a2=4,b2=1.
∴椭圆方程为$\frac{{x}^{2}}{4}$+y2=1.
故答案为:$\frac{{x}^{2}}{4}$+y2=1.
点评 本题考查了椭圆的标准方程及其性质、数量积运算性质、点与椭圆的位置关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.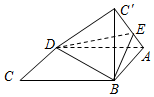 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |