题目内容
17.已知正项等比数列{an}的前n项积为πn,已知am-1•am+1=2am,π2m-1=2048,则m=6.分析 由am-1am+1-2am=0,结合等比数列的性质可得am=2,从而可表示T2m-1,由此可求m的值.
解答 解:∵am-1am+1=2am,∴由等比数列的性质可得,am2-2am=0,
∵am>0,∴am=2,
∵π2m-1=a1a2…a2m-1=(a1a2m-1)•(a2a2m-2)…am=am2m-2am=am2m-1=22m-1=2048,
∴2m-1=11,∴m=6.
故答案为:6.
点评 本题考查了等比数列的性质,考查学生的计算能力,属于中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
7.下列命题中,正确的是( )
| A. | θ=$\frac{π}{4}$是f(x)=sin(x-2θ)的图象关于y轴对称的充分不必要条件 | |
| B. | |a|-|b|=|a-b|的充要条件是a与b的方向相同 | |
| C. | b=$\sqrt{ac}$是a,b,c三数成等比数列的充分不必要条件 | |
| D. | m=3是直线(m+3)x+my-2=0与mx-6y+5=0互相垂直的充要条件 |
8.在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
| A. | (-2,-1) | B. | (-1,0) | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
6.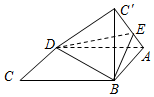 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
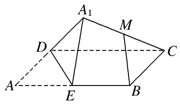 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)