题目内容
20．已知f（x）=$\left\{\begin{array}{l}{x-4，（x≥6）}\\{f（x+2），（x＜6）}\end{array}\right.$，则f（3）=3．分析 利用函数性质得f（3）=f（5）=f（7），由此能求出结果．
解答 解：∵f（x）=$\left\{\begin{array}{l}{x-4，（x≥6）}\\{f（x+2），（x＜6）}\end{array}\right.$，
∴f（3）=f（5）=f（7）=7-4=3．
故答案为：3．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
智能训练练测考系列答案
相关题目
8．在下列区间中，函数f（x）=ex+4x-3的零点所在的区间为（ ）
| A． | （-2，-1） | B． | （-1，0） | C． | $（0，\frac{1}{2}）$ | D． | $（\frac{1}{2}，1）$ |
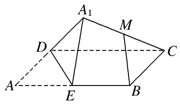如图，矩形ABCD中，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中，下列说法正确的是①②．（填序号）