题目内容
函数y=lg(3-
)的定义域是 .
| 1 |
| x |
考点:对数函数的定义域
专题:函数的性质及应用
分析:直接由对数式的真数大于0求解x的取值集合得答案.
解答:
解:由3-
>0,得
>0,解得x<0或x>
.
∴函数y=lg(3-
)的定义域是{x|x<0或x>
}.
故答案为:{x|x<0或x>
}.
| 1 |
| x |
| 3x-1 |
| x |
| 1 |
| 3 |
∴函数y=lg(3-
| 1 |
| x |
| 1 |
| 3 |
故答案为:{x|x<0或x>
| 1 |
| 3 |
点评:本题考查了函数的定义域及其求法,是基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知抛物线C:y2=4x的焦点为F,过点F的直线l交抛物线于M,N两点,且|MF|=2|NF|,则直线l的斜率为( )
A、±
| ||||
B、±2
| ||||
C、±
| ||||
D、±
|
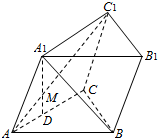 如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=a,点A1在底面ABC上的射影恰为AC的中点D,A1D∩AC1=M,BA1⊥AC1.