题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且bcosC=(3a-c)cosB.
(Ⅰ)求cosB的值.
(Ⅱ)若b=
,c=
,求△ABC的面积.
(Ⅰ)求cosB的值.
(Ⅱ)若b=
| 3 |
| ||
| 2 |
考点:余弦定理的应用
专题:综合题,解三角形
分析:(Ⅰ)由正弦定理与两角和与差的展开式进行计算,可得cosB的值.
(Ⅱ)根据余弦定理求出边长a,再利用三角形面积公式,即可求△ABC的面积.
(Ⅱ)根据余弦定理求出边长a,再利用三角形面积公式,即可求△ABC的面积.
解答:
解:(Ⅰ)由正弦定理得a=2RsinA,b=2RsinB,c=2RsinC,
又bcosC=3acosB-ccosB,
所以sinBcosC=3sinAcosB-sinCcosB,即sin(B+C)=3sinAcosB,
所以cosB=
;
(Ⅱ)因为b=
,c=
,
所以a=
,又sinB=
=
,
所以S△ABC=
acsinB=
.
又bcosC=3acosB-ccosB,
所以sinBcosC=3sinAcosB-sinCcosB,即sin(B+C)=3sinAcosB,
所以cosB=
| 1 |
| 3 |
(Ⅱ)因为b=
| 3 |
| ||
| 2 |
所以a=
| 6 |
| 1-cos2B |
| ||
| 4 |
所以S△ABC=
| 1 |
| 2 |
| 3 |
| 8 |
| 7 |
点评:本题考查弦定理与两角和与差的公式,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
二项式(x2-
)9的展开式中的常数项为( )
| 1 |
| x |
| A、36 | B、-36 |
| C、84 | D、-84 |
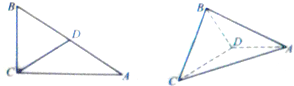 在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD.
在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD. 已知某几何体的三视图如图所示,其中侧视图是边长为2的正三角形,正视图是矩形,且AA1=4,则此几何体的体积为
已知某几何体的三视图如图所示,其中侧视图是边长为2的正三角形,正视图是矩形,且AA1=4,则此几何体的体积为