题目内容

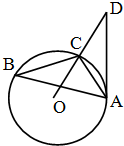如图，已知△ABC内接于圆O，点D在OC的延长线上，AD切圆O于A，若∠ABC=30°，AC=2，则AD的长为
 
．
考点：与圆有关的比例线段
专题：直线与圆
分析：作CE⊥AD于点E，由已知结合三角形中角的关系得到AE的长度，再由AD=2AE得答案．
解答： 解：如图，作CE⊥AD于点E，
∵∠ABC=30°，∴∠CDA=30°，则∠COA=60°，
∴△AOC为正三角形，
∴∠CAO=60°，AC=OC，
∴∠CAE=30°，AC=CD，
又∵CE⊥AD，
∴AE=
3
2
AC=3
3
，
则AD=2AE=6
3
．
故答案为：6
3
．
点评：本题考查了与圆有关的比例线段，考查了直角三角形的解法，是中档题．
练习册系列答案
相关题目
若函数f（x）=
1
x
，x＜0
(
1
3
)x，x≥0
，则不等式-
1
3
≤f（x）≤
1
3
的解集为（　　）
A、[-1，2）∪[3，+∞）
B、（-∞，-3]∪[1，+∞）
C、[
3
2
，+∞）
D、（1，
3
]∪[3，+∞）
已知点P（m，4）是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的一点，F1，F2是椭圆的两个焦点，若△PF1F2的内切圆的半径为
3
2
，则此椭圆的离心率为
 
．
已知数列{an}是公差不为0的等差数列，其前n项和为Sn，a1，a2，a4成等比数列，2a5=S3+8
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}的前n项和Tn=
3n
an+1
，对任意n≥2且n∈N*，不等式bn＜kTn恒成立，求实数k的取值范围．
四面体ABCD的外接球为O，AD⊥平面ABC，AD=2，∠ACB=30°，AB=
3
，则球O的表面积为（　　）
A、32π
B、16π
C、12π
D、
22
3
π
写出角的终边在图中阴影区域内角的集合（包括边界）
已知异面直线a，b均与平面α相交，下列命题：
（1）存在直线m?α，使得m⊥a或m⊥b．
（2）存在直线m?α，使得m⊥a且m⊥b．
（3）存在直线m?α，使得m与a和b所成的角相等．
其中不正确的命题个数为（　　）
A、0B、1C、2D、3
已知函数f（x）=
1
3
x3+3xf′（a），f（a）=
7
6
，则a=
 
．
如图，双曲线
x2
a2
-
y2
b2
=1（a＞b＞0）的两个焦点分别为F1、F2，以F1、F2为边作等边三角形MF1F2．若双曲线恰好平分三角形的另两边，则双曲线的离心率为（　　）
A、1+
3
B、4+2
3
C、2
3
-2
D、2
3
+2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网