题目内容
4．等差数列{an}满足a1=39，a1+a3=74，则通项公式an=（ ）| A． | -2n+41 | B． | -2n+39 | C． | -n2+40n | D． | -n2-40n |
分析 利用等差数列通项公式列出方程，求出公差，由此能求出结果．
解答 解：∵等差数列{an}满足a1=39，a1+a3=74，
∴39+39+2d=74，
解得d=-2，
∴通项公式an=39+（n-1）×（-2）=-2n+41．
故选：A．
点评 本题考查等差数列的通项公式的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
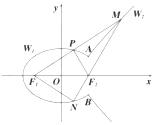如图：椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）有相同的焦点F1、F2，它们在y轴右侧有两个交点A、B，满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0．将直线AB左侧的椭圆部分（含A，B两点）记为曲线W1，直线AB右侧的双曲线部分（不含A，B两点）记为曲线W2．以F1为端点作一条射线，分别交W1于点P（xP，yP），交W2于点M（xM，yM）（点M在第一象限），设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$．