题目内容
14.如图1,菱形ABCD的边长为12,∠BAD=60°,AC与BD交于O点.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=6$\sqrt{2}$.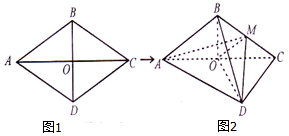
( I)求证:平面ODM⊥平面ABC;
( II)求二面角M-AD-C的余弦值.
分析 (Ⅰ)推导出OD⊥AC,DO⊥OM,从而OD⊥面ABC,由此能证明平面ODM⊥平面ABC.
(Ⅱ)由OD⊥OC,OB⊥OC,OB⊥OD,建立空间直角坐标系,利用向量法能求出二面角M-AD-C的余弦值.
解答 (本小题满分12分)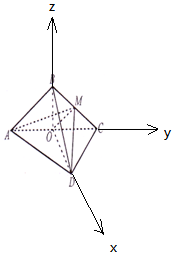
证明:(Ⅰ)∵ABCD是菱形,
∴AD=DC,OD⊥AC,
△ADC中,AD=DC=12,∠ADC=120°,
∴OD=6,
又M是BC中点,∴$OM=\frac{1}{2}AB=6,MD=6\sqrt{2}$,
∵OD2+OM2=MD2,∴DO⊥OM,
∵OM,AC?面ABC,OM∩AC=O,
∴OD⊥面ABC,
又∵OD?平面ODM,∴平面ODM⊥平面ABC.…(6分)
解:(Ⅱ)由题意,OD⊥OC,OB⊥OC,
又由(Ⅰ)知OB⊥OD,建立如图所示空间直角坐标系,
由条件知:$D({6,0,0}),A({0,-6\sqrt{3},0}),M({0,3\sqrt{3},3})$
故$\overrightarrow{AM}=({0,9\sqrt{3},3}),\overrightarrow{AD}=({6,6\sqrt{3},0})$,
设平面MAD的法向量$\overrightarrow m=({x,y,z})$,
则 $\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{AM}=0\\ \overrightarrow m•\overrightarrow{AD}=0\end{array}\right.$,即$\left\{\begin{array}{l}9\sqrt{3}y+3z=0\\ 6x+6\sqrt{3}y=0\end{array}\right.$,令$y=-\sqrt{3}$,则x=3,z=9
∴$\overrightarrow m=({3,-\sqrt{3},9})$
由条件知OB⊥平面ACD,故取平面ACD的法向量为$\overrightarrow n=({0,0,1})$
所以,$cos\left?{\overrightarrow m,\overrightarrow n}\right>=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{{3\sqrt{93}}}{31}$
由图知二面角M-AD-C为锐二面角,
故二面角M-AD-C的余弦值为$\frac{{3\sqrt{93}}}{31}$.(12分)
点评 本题考查面面垂直的证明,考查二面角的余弦值的求法,考查推理论证能力、空间思维能力、运算求解能力,考查等价转化思想、数形结合思想,是中档题.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案| A. | -2n+41 | B. | -2n+39 | C. | -n2+40n | D. | -n2-40n |
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
| A. | 15 | B. | 20 | C. | 25 | D. | 15或25 |
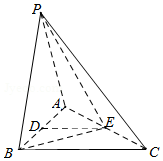 如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$
如图:等边三角形PAB所在的平面与Rt△ABC所在的平面互相垂直,D、E分别为AB、AC边中点.已知AB⊥BC,AB=2,BC=2$\sqrt{3}$