题目内容
17.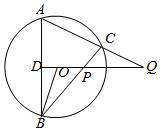 如图,A,B,C是圆O上不共线的三点,OD⊥AB于D,BC和AC分别交DO的延长线于P和Q,求证:∠OBP=∠CQP.
如图,A,B,C是圆O上不共线的三点,OD⊥AB于D,BC和AC分别交DO的延长线于P和Q,求证:∠OBP=∠CQP.
分析 连接OA,推出∠ACB=∠DOB,证明∠BOP=∠QCP,说明B,O,C,Q四点共圆,证明即可.
解答  [选修4-1:几何证明选讲](本小题满分10分)
[选修4-1:几何证明选讲](本小题满分10分)
证明:连接OA,因为OD⊥AB,OA=OB,所以$∠BOD=∠AOD=\frac{1}{2}∠AOB$,
又$∠ACB=\frac{1}{2}∠AOB$,所以∠ACB=∠DOB,…(5分)
又因为∠BOP=180°-∠DOP,∠QCP=180°-∠ACB,所以
∠BOP=∠QCP,所以B,O,C,Q四点共圆,
所以∠OBP=∠CQP.…(10分)
点评 本题考查直线与圆的位置关系,四点共圆的应用,考查转化思想以及逻辑推理能力.

练习册系列答案
相关题目
6.某高中要从该校三个年级中各选取1名学生参加校外的一项知识问答活动,若高一、高二、高三年级分别有5,6,8个学生备选,则不同选法有( )
| A. | 19种 | B. | 38种 | C. | 120种 | D. | 240种 |
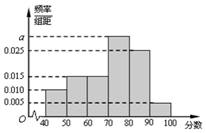 某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.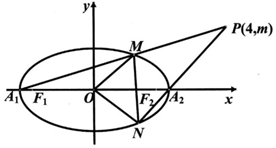 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.