题目内容
14.在△ABC中,AB=5,BC=2,∠B=60°,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )| A. | 5$\sqrt{3}$ | B. | 5 | C. | -5$\sqrt{3}$ | D. | 20 |
分析 由题意画出图形,把$\overrightarrow{AB}$•$\overrightarrow{AC}$转化为含有$\overrightarrow{BA}、\overrightarrow{BC}$的式子化简求值.
解答 解:如图,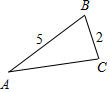
∵AB=5,BC=2,∠B=60°,
∴$\overrightarrow{AB}•\overrightarrow{AC}$=$\overrightarrow{AB}•(\overrightarrow{BC}-\overrightarrow{BA})$=$\overrightarrow{AB}•\overrightarrow{BC}+{\overrightarrow{BA}}^{2}=5×2×cos120°+25$=-5+25=20.
故选:D.
点评 本题考查平面向量的数量积运算,考查向量减法的三角形法则,是基础的计算题.

练习册系列答案
相关题目
6.已知$f(x)=sin[\frac{π}{3}(x+1)]-\sqrt{3}cos[\frac{π}{3}(x+1)]$,则f(1)+f(2)+f(3)+…+f(2013)=( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
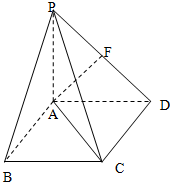 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.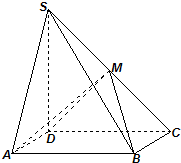 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
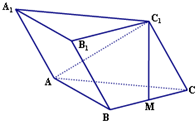 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.