题目内容
18.设a、b为正数,$\frac{1}{a}$+$\frac{1}{b}$≤2$\sqrt{2}$,(a-b)2=4(ab)3,则a+b=( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 令s=a+b,t=ab,得到$\frac{\sqrt{2}}{4}$s≤t,由(a-b)2=4(ab)3,可以得到s2-4t=4t3,即可得到s2-4$\sqrt{2}$s+8≤0,解得即可.
解答 解:令s=a+b,t=ab
则由 $\frac{1}{a}$+$\frac{1}{b}$≤2$\sqrt{2}$,得$\frac{\sqrt{2}}{4}$s≤t,
由(a-b)2=4(ab)3,得(a+b)2-4ab=4(ab)3,
∴s2-4t=4t3,
即s2=4t+4t3≥$\sqrt{2}$s+$\frac{\sqrt{2}}{8}$s3,
即s2-4$\sqrt{2}$s+8=(s-2$\sqrt{2}$)2≤0,
解之得s=2$\sqrt{2}$.
则a+b的值等于2$\sqrt{2}$.
故选:C.
点评 本题考查了不等式的应用,关键是换元,以及转化,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
6.已知$f(x)=sin[\frac{π}{3}(x+1)]-\sqrt{3}cos[\frac{π}{3}(x+1)]$,则f(1)+f(2)+f(3)+…+f(2013)=( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
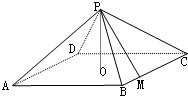 如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,
如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,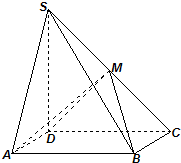 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.