题目内容
△ABC的内角A、B、C的对边分别为a、b、c，若a=2，b=2
，A=30°，则B等于（ ）
| 3 |
| A、60° |
| B、60°或l20° |
| C、30° |
| D、30°或l50° |
考点：正弦定理
专题：计算题,解三角形
分析：由A的度数求出sinA的值，然后再由a与b的值，利用正弦定理求出sinB的值，根据A的度数及三角形的内角和定理确定出B的范围，利用特殊角的三角函数值即可求出满足题意的B的度数．
解答：
解：由a=2，b=2
，A=30°，
根据正弦定理
=
得：
sinB=
=
=
，
又B为三角形的内角，且A=30°，
得到B∈（0°，150°），
则B等于60°或120°．
故选B．
| 3 |
根据正弦定理
| a |
| sinA |
| b |
| sinB |
sinB=
| bsinA |
| a |
2
| ||||
| 2 |
| ||
| 2 |
又B为三角形的内角，且A=30°，
得到B∈（0°，150°），
则B等于60°或120°．
故选B．
点评：此题考查了解三角形的知识，用到的知识有正弦定理，以及特殊角的三角函数值，学生在做题时利用正弦定理求出sinB的值后，注意根据A的度数及三角形的内角和定理确定出B的度数范围，从而利用特殊角的三角函数值求出满足题意的B的度数．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知数列{an}，an+1=kan+3（k＞0），其中a1=0，a4=9，则k等于（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
复数z=
的共轭复数是（ ）
| i |
| 1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知sin（π+α）=
，则cos（
-α）=（ ）
| 1 |
| 3 |
| 3π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
将角-
π写成α+2kπ（k∈Z，0≤α＜2π）的形式，正确的是（ ）
| 27 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
在△ABC中，角A，B，C所对的边分别为5，7，8，则∠B的大小是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若点A（1，m-1，1）和点B（-1，-3，-1）关于原点对称，则m=（ ）
| A、-4 | B、4 | C、2 | D、-2 |
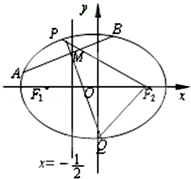如图，F1，F2是离心率为