Question

1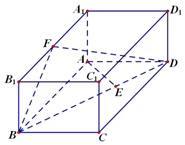．如图，已知长方体ABCD-A₁B₁C₁D₁，AB=2，AA₁=1，直线BD与平面AA₁B₁B所成的角为30°，AE垂直BD于点E，F为A₁B₁的中点．
（1）求异面直线AE与BF所成角的余弦值；
（2）求平面BDF与平面AA₁B₁B所成二面角（锐角）的余弦值．

Answer 1

分析 （1）以AB所在直线为x轴，AD所在直线为y轴，AA₁所在直线为z轴，建立空间直角坐标系，利用向量法能求出异面直线AE、BF所成的角的余弦值．
（2）分别求出平面AA₁B的一个法向量和平面BDF的一个法向量，由此利用向量法能求出平面BDF与平面AA₁B所成的二面角（锐角）的余弦值．

解答 解：（1）在长方体ABCD-A₁B₁C₁D₁中，
以AB所在直线为x轴，AD所在直线为y轴，AA₁所在直线为z轴，建立空间直角坐标系，如图．
由已知AB=2，AA₁=1，可得A（0，0，0），B（2，0，0），F（1，0，1）．                                                               
又AD⊥平面AA₁B₁B，从而BD与平面AA₁B₁B所成的角为∠DBA=30°．
又AB=2，AE⊥BD，AE=1，AD=$\frac{2\sqrt{3}}{3}$，由已知得得E（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$，0），D（0，$\frac{2\sqrt{3}}{3}$，0）
$\overrightarrow{BF}$=（-1，0，1），$\overrightarrow{AE}=（\frac{1}{2}，\frac{\sqrt{3}}{2}，0）$，∴$cos＜\overrightarrow{AE}，\overrightarrow{BF}＞=-\frac{\sqrt{2}}{4}$，
即异面直线AE、BF所成的角的余弦值为$\frac{\sqrt{2}}{4}$．
（2）平面AA₁B的一个法向量为$\overrightarrow{m}$=（0，1，0）．
设$\overrightarrow{n}$=（x，y，z）是平面BDF的一个法向量，$\overrightarrow{BD}=（-2，\frac{2\sqrt{3}}{3}，0）$．
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BF}=-x+z=0}\\{\overrightarrow{n}•\overrightarrow{BD}=2x-\frac{2\sqrt{3}}{3}y=0}\end{array}\right.$，取$\overrightarrow{n}=（1，\sqrt{3}，1）$．
∴所以cos$＜\overrightarrow{m}，\overrightarrow{n}＞$=$\frac{\sqrt{15}}{5}$．
平面BDF与平面AA₁B₁B所成二面角（锐角）的余弦值为$\frac{\sqrt{15}}{5}$．

点评 本题考查异面直线所成角的余弦值的法，考查二面角的余弦值的求法，是中档题，解题时要认真审题，注意向量法的合理运用．属于中档题．