题目内容
11.在直角坐标系xOy中,直线l的斜率为$\sqrt{3}$,且与x轴交于点M(-1,0),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2-4ρsinθ+3=0.(1)求直线l的参数方程和曲线C的直角坐标方程;
(2)直线l与曲线C交于A,B两点,求|MA|+|MB|的值.
分析 (1)根据极坐标和参数方程的定义进行求解即可.
(2)设A,B对应的参数分别为t1,t2,联立方程求出结合|MA|+|MB|=|t1|+|t2|进行计算即可.
解答 解:(1)直线l的斜率为$\sqrt{3}$,且与x轴交于点M(-1,0),∴直线l的参数方程为$\left\{\begin{array}{l}{x=-1+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t是参数);
由ρ2-4ρsinθ+3=0得x2+y2-4y+3=0⇒x2+(y-2)2=1;
(2)设A,B对应的参数分别为t1,t2,把直线的参数方程代入曲线方程得(-1-$\frac{1}{2}$t)2+($\frac{\sqrt{3}}{2}$t-2)2=1,
整理得t2-(2$\sqrt{3}$+1)t+4=0,
则t1+t2=2$\sqrt{3}$+1,t1t2=4,
∴t1>0,t2>0,
则|MA|+|MB|=|t1|+|t2|=|t1|+|t2|=2$\sqrt{3}$+1.
点评 本题主要考查参数方程,极坐标方程的应用,根据相应的转换公式进行化简是解决本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
19.已知等差数列{an}的公差d不为零,前n项和是Sn,若a3,a5,a10成等比数列,则( )
| A. | a1d>0,dS4>0 | B. | a1d>0,dS4<0 | C. | a1d<0,dS4>0 | D. | a1d<0,dS4<0 |
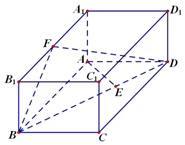 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.