题目内容
9.化简$\frac{tan(45°-α)}{1-tan{\;}^{2}(45°-α)}$•$\frac{sinαcosα}{cos{\;}^{2}α-sin{\;}^{2}α}$=$\frac{1}{4}$.分析 运用倍角公式化简各因数.
解答 解:原式=$\frac{1}{2}$tan2(45°-α)•$\frac{\frac{1}{2}sin2α}{cos2α}$=$\frac{1}{4}$cot2αtan2α=$\frac{1}{4}$;
故答案为:$\frac{1}{4}$.
点评 本题考查了三角函数的化简求值;熟练运用倍角公式是关键.

练习册系列答案
相关题目
19.已知等差数列{an}的公差d不为零,前n项和是Sn,若a3,a5,a10成等比数列,则( )
| A. | a1d>0,dS4>0 | B. | a1d>0,dS4<0 | C. | a1d<0,dS4>0 | D. | a1d<0,dS4<0 |
17.已知α是锐角,$\overrightarrow a=({\frac{3}{4},sinα}),\overrightarrow b=({cosα,\frac{1}{{\sqrt{3}}}})$,且$\overrightarrow a$∥$\overrightarrow b$,则α为( )
| A. | 15o | B. | 30o | C. | 30o或60o | D. | 15o或75o |
19.某算法的程序框图如图所示,若输x的值为2,则输出y的值是( )
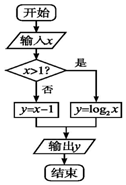

| A. | 1 | B. | 2 | C. | 4 | D. | 以上都不对 |
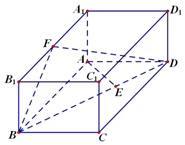 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.