题目内容
6.在三棱锥P-ABC中,侧面PAB,侧面PAC,侧PBC两两互相垂直,且$PA:PB:PC=1:\sqrt{2}:\sqrt{3}$,设三棱锥P-ABC的体积为V1,三棱锥P-ABC的外接球的体积为V2,则$\frac{V_2}{V_1}$=( )| A. | $\frac{{7\sqrt{14}}}{3}π$ | B. | 6π | C. | 3π | D. | $\frac{8}{3}π$ |
分析 三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,它的外接球就是它扩展为长方体的外接球,求出长方体的对角线的长,就是球的直径,然后求球的体积V2.三棱锥P-ABC的体积为V1即可.
解答 解:∵三棱锥P-ABC中,侧面PAB,侧面PAC,侧PBC两两互相垂直,即三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,它的外接球就是它扩展为长方体的外接球,求出长方体的对角线的长,就是球的直径;
∵$PA:PB:PC=1:\sqrt{2}:\sqrt{3}$,设PA=1,则三棱锥P-ABC的体积为V1=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{2}×\sqrt{3}=\frac{\sqrt{6}}{6}$.
三棱锥P-ABC的外接球的半径R=$\frac{\sqrt{{1}^{1}+(\sqrt{2})^{2}+(\sqrt{3})^{2}}}{2}=\frac{\sqrt{6}}{2}$,体积为V2=$\frac{4}{3}π{R}^{2}=\sqrt{6}π$,
则$\frac{V_2}{V_1}$=6π.
故选:B
点评 本题考查球的体积,几何体的外接球,考查空间想象能力,计算能力,是基础题.

练习册系列答案
相关题目
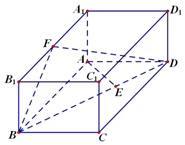 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于点E,F为A1B1的中点.