题目内容
15.已知函数f(x)=3x,f(a+2)=81,g(x)=$\frac{{1-{a^x}}}{{1+{a^x}}}$.(1)求g(x)的解析式并判断函数g(x)的奇偶性;
(2)求函数g(x)的值域.
分析 (1)根据题意,由f(a+2)=81可得3a+2=81,解可得a的值,即可得函数g(x)的解析式,结合g(x)的解析式,先分析其定义域,再分析g(-x)与g(x)的关系,即可得答案;
(2)由(1)得到g(x)的解析式,将其变形可得g(x)=$\frac{2}{1+{2}^{x}}$-1,结合指数函数的性质分析即可得答案.
解答 解:(1)由f(a+2)=3a+2=81,得a+2=4,故a=2;
所以$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}$;
对于$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}$,其定义域为R,
而又由$g({-x})=\frac{{1-{2^{-x}}}}{{1+{2^{-x}}}}=\frac{{{2^x}-1}}{{{2^x}+1}}=-\frac{{1-{2^x}}}{{{2^x}+1}}=-g(x)$,
所以函数g(x)为奇函数;
(2)$g(x)=\frac{{1-{2^x}}}{{1+{2^x}}}=\frac{{2-(1+{2^x})}}{{1+{2^x}}}=\frac{2}{{1+{2^x}}}-1$,
${2^x}∈(0,+∞)⇒{2^x}+1∈(1,+∞)⇒\frac{1}{{{2^x}+1}}∈(0,1)$,
所以$\frac{2}{{{2^x}+1}}$$∈(0,2)⇒\frac{2}{{1+{2^x}}}-1∈(-1,1)$,
即函数g(x)的值域为(-1,1).
点评 本题考查函数的单调性、奇偶性的判定与应用,判定奇偶性之前要先分析函数的定义域.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
6.在一个个体数目为1002的总体中,要利用系统抽样抽取一个容量为50的样本,先用简单随机抽样删除两个个体,然后再从这1000个个体中抽50个个体,在这个过程中,每个个体被抽到的概率为( )
| A. | $\frac{1}{20}$ | |
| B. | $\frac{50}{1002}$ | |
| C. | $\frac{1}{1001}$ | |
| D. | 有两个个体与其它个体被抽到的概率不相等 |
20.在△ABC中,∠C=90°,且CA=CB=3,点M满足$\overrightarrow{BM}$=2$\overrightarrow{AM}$,则$\overrightarrow{CM}$$•\overrightarrow{CA}$=( )
| A. | 18 | B. | 3 | C. | 15 | D. | 9 |
5.如图是一个棱锥的三视图,则该棱锥的体积为( )


| A. | 12 | B. | 4 | C. | 6 | D. | 2 |
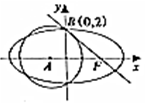 如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.
如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.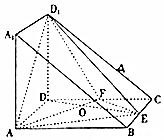 将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.
将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.