题目内容
椭圆 与双曲线
与双曲线 有公共的焦点,过椭圆
有公共的焦点,过椭圆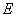 的右焦点作任意直线
的右焦点作任意直线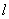 ,设直线
,设直线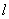 交抛物线
交抛物线 于
于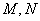 两点,且
两点,且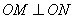
(1)求椭圆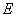 的方程;
的方程;
(2)设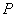 是椭圆
是椭圆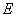 上第一象限内的点,点
上第一象限内的点,点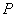 关于原点
关于原点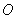 的对称点为
的对称点为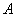 ,关于
,关于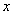 轴的对称点为
轴的对称点为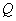 ,线段
,线段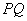 与x轴相交于点
与x轴相交于点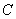 ,点
,点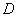 为
为 的中点,若直线
的中点,若直线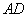 与椭圆
与椭圆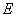 的另一个交点为
的另一个交点为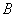 ,试判断直线
,试判断直线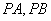 是否相互垂直?并证明你的结论。
是否相互垂直?并证明你的结论。
解:(1)设点 ,
,
设直线
 ,代入
,代入 并整理得
并整理得
所以
故有


 解得
解得
又椭圆与双曲线有公共的焦点,故有
所以椭圆的方程为 .
.
(2) 
证明:设 ,则
,则 ,
, 且
且
将直线 的方程
的方程 代入椭圆的方程并整理得
代入椭圆的方程并整理得

由题意可知此方程必有一根
 ,
, 

所以
故有 , 即
, 即

练习册系列答案
相关题目

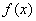 的最小正周期和函数在
的最小正周期和函数在 上的单调减区间;
上的单调减区间; 中,
中, ,求角
,求角 .
. 中,
中, 为
为 上一点,且
上一点,且 ,
, 为
为 上一点,且
上一点,且 ,则
,则 取最小值时,向量
取最小值时,向量
 的模为 .
的模为 . 的焦点
的焦点 ,交抛物线
,交抛物线 两点,且点
两点,且点 轴的距离相等
轴的距离相等 ,则
,则 的最大值为( )
的最大值为( ) B.
B. C.4 D.6
C.4 D.6 
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 上的最大值和最小值,并求出相应的
上的最大值和最小值,并求出相应的 中任取一点
中任取一点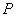 ,则点
,则点 围成的区域内(阴影部分)的概率为( )
围成的区域内(阴影部分)的概率为( ) B.
B. C.
C. D.
D.



 ,则
,则 或
或 ”的否定是( )
”的否定是( ) 或
或 B.若
B.若 ,则
,则