题目内容
已知命题p:x>1是|x|>1成立的充分不必要条件;命题q:若不等式|x+1|+|x-2|>a对?x∈R恒成立,则a≤3,在命题①p∧q ②p∨q ③p∧(-q) ④(-p)∨q中,真命题是( )
| A、②③ | B、②④ | C、①③ | D、①④ |
考点:复合命题的真假
专题:简易逻辑
分析:分别判断命题p,q的真假关系,利用复合命题和简单命题之间的关系进行判断.
解答:
解:命题p:x>1是|x|>1成立的充分不必要条件是真命题,不等式|x+1|+|x-2|>a对?x∈R恒成立,则a<3是真命题,故命题q是假命题,
故②p∨q、③p∧(-q)是真命题.
故选A:.
故②p∨q、③p∧(-q)是真命题.
故选A:.
点评:本题主要考查复合命题与简单命题真假关系的判断,比较基础.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知θ为第一象限角,设向量
=(sinθ,
),向量
=(cosθ,3),且
∥
,则θ一定为( )
| a |
| 3 |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
点A(-1,2)关于直线x+y+3=0的对称点B的坐标为( )
| A、(-5,-2) |
| B、(2,5) |
| C、(-2,-5) |
| D、(5,2) |
设集合S={x||x|<5},T={x|(x+7)(3-x)>0},则S∩T=( )
| A、{x|-7<x<-5} |
| B、{x|3<x<5} |
| C、{x|-5<x<3} |
| D、{x|-7<x<5} |
设向量a=(2,0),b=(1,1),则下列结论中正确的是( )
| A、|a|=|b| | ||
B、a=(2,0)•b=(1,1)=
| ||
| C、a∥b | ||
| D、(a-b)⊥b |
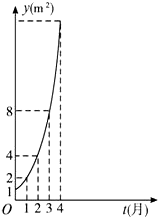 如图所示是某池塘中浮萍的面积y(m2)与时间t(月)的关系y=f(t)=at,有以下叙述:
如图所示是某池塘中浮萍的面积y(m2)与时间t(月)的关系y=f(t)=at,有以下叙述: