题目内容
已知sinα、cosα是一元二次方程2x2+ax+b=0的两个根,则点(a,b)的轨迹的普通方程是 .
考点:轨迹方程,参数方程化成普通方程
专题:圆锥曲线的定义、性质与方程,坐标系和参数方程
分析:利用韦达定理化简求得a、b的关系式,消去α即可得到点(a,b)的轨迹的普通方程.
解答:
解:由题意利用韦达定理可得sinα+cosα=-
a…①,sinα•cosα=
…②,
①2可得:1+2sinαcosα=
a2,②代入表达式可得:1+b=
a2,
即b=
a2-1.
所求轨迹方程为:b=
a2-1.
故答案为:b=
a2-1.
| 1 |
| 2 |
| b |
| 2 |
①2可得:1+2sinαcosα=
| 1 |
| 4 |
| 1 |
| 4 |
即b=
| 1 |
| 4 |
所求轨迹方程为:b=
| 1 |
| 4 |
故答案为:b=
| 1 |
| 4 |
点评:本题主要考查轨迹方程的求法,韦达定理、参数方程的应用,属于中档题.

练习册系列答案
相关题目
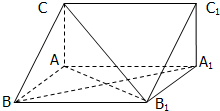 直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB= 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G. 已知函数f(x)=2sin(ωx+φ),x∈R(其中ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ),x∈R(其中ω>0,|φ|<