题目内容
将长度为l(l≥4,l∈N*)的线段分成n(n≥3)段,每段长度均为正整数,并要求这n段中的任意三段都不能构成三角形.例如,当l=4时,只可以分为长度分别为1,1,2的三段,此时n的最大值为3;当l=7时,可以分为长度分别为1,2,4的三段或长度分别为1,1,1,3的四段,此时n的最大值为4.则:
(1)当l=12时,n的最大值为 ;
(2)当l=100时,n的最大值为 .
(1)当l=12时,n的最大值为
(2)当l=100时,n的最大值为
考点:进行简单的合情推理
专题:推理和证明
分析:若这n段中的任意三段都不能构成三角形,则分成的n段中,首先取2个1分米,后面的数依次是前面两个数的和,依次即可求解.
解答:
解:(1)当l=12时,n的最大值为5,
此时能分成的n段的长度分别是1、1、1+1=2、1+2=3、2+3=5,
(2)当l=100时,n的最大值为9,
此时能分成的n段的长度分别是1、1、1+1=2、1+2=3、2+3=5,3+5=8,5+8=13,8+13=21,46
故答案为:5,9
此时能分成的n段的长度分别是1、1、1+1=2、1+2=3、2+3=5,
(2)当l=100时,n的最大值为9,
此时能分成的n段的长度分别是1、1、1+1=2、1+2=3、2+3=5,3+5=8,5+8=13,8+13=21,46
故答案为:5,9
点评:考查了三角形三边关系定理:三角形两边之和大于第三边.

练习册系列答案
相关题目
设双曲线
-
=1(a>0,b>0)的离心率e=2,右焦点F(c,0),方程ax2+bx-c=0的两个根分别为x1,x2,则点P(x1,x2)在( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、圆x2+y2=10内 |
| B、圆x2+y2=10上 |
| C、圆x2+y2=10外 |
| D、以上三种情况都有可能 |
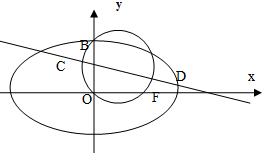 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x- 如图所示,已知圆C:(x+1)2+y2=8,A(1,0)为定点,B为圆C上的动点,线段AB的垂直平分线交BC于点D,点D的轨迹为曲线E.
如图所示,已知圆C:(x+1)2+y2=8,A(1,0)为定点,B为圆C上的动点,线段AB的垂直平分线交BC于点D,点D的轨迹为曲线E.