题目内容
求下列函数的解析式:
(1)已知f(x)为一次函数,且f[f(x)]=4x-1,求f(x);
(2)已知f(
+1)=x+2
,求f(x).
(1)已知f(x)为一次函数,且f[f(x)]=4x-1,求f(x);
(2)已知f(
| x |
| x |
考点:函数解析式的求解及常用方法
专题:待定系数法,配方法,函数的性质及应用
分析:(1)用待定系数法,设出f(x)=ax+b,求出系数a、b即可;
(2)利用配方法,求出f(
+1)=(
+1)2-1,即得f(x).
(2)利用配方法,求出f(
| x |
| x |
解答:
解:(1)根据题意,设f(x)=ax+b,ab∈R,
∴f[f(x)]=f[ax+b]=a(ax+b)+b=a2x+ab+b=4x-1,
∴
,
解得
,或
;
∴f(x)=2x-
,或f(x)=-2x+1;
(2)∵f(
+1)=x+2
=(
+1)2-1,
且
≥0,
∴
+1≥1;
∴f(x)=x2-1,其中x≥1.
∴f[f(x)]=f[ax+b]=a(ax+b)+b=a2x+ab+b=4x-1,
∴
|
解得
|
|
∴f(x)=2x-
| 1 |
| 3 |
(2)∵f(
| x |
| x |
| x |
且
| x |
∴
| x |
∴f(x)=x2-1,其中x≥1.
点评:本题考查了求函数解析式的常用方法问题,解题时应根据题意,选择适当地方法进行解答,是基础题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
将编号为1,2,3,4,5,6的6张卡片,放入四个不同的盒子中,每个盒子至少放入一张卡片,则编号为3与6的卡片恰在同一个盒子中的不同放法共有( )
| A、120 | B、240 |
| C、360 | D、480 |
已知等差数列{an}满足a1+a2+a3+…+a101=0,则a1+a101与0的大小关系为( )
| A、a1+a101>0 |
| B、a1+a101<0 |
| C、a1+a101=0 |
| D、以上皆有可能 |
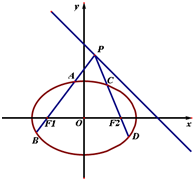 已知椭圆
已知椭圆