题目内容
12.已知等差数列{an}的前n项和为Sn,a2=2,S5=15,则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前2017项和为( )| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2017}$ |
分析 设等差数列{an}的公差为d,由a2=2,S5=15,可得a1+d=2,$5{a}_{1}+\frac{5×4}{2}$d=15,解得a1,d,可得an,即可得出.
解答 解:设等差数列{an}的公差为d,∵a2=2,S5=15,
∴a1+d=2,$5{a}_{1}+\frac{5×4}{2}$d=15,解得a1=d=1,
∴an=1+(n-1)=n.
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前2017项和=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{2017}-\frac{1}{2018})$=1-$\frac{1}{2018}$=$\frac{2017}{2018}$.
故选:C.
点评 本题考查了等差数列的通项公式与求和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知函数f(x)=$\left\{\begin{array}{l}{-\sqrt{x},x>0}\\{(x-\frac{1}{x})^{4},x<0}\end{array}\right.$,则f(f(2))=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
 如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.
如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.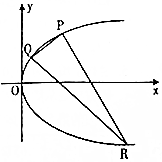 已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.
已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.