题目内容
10.已知角θ的终边过点P(-12,5),则cosθ=( )| A. | $\frac{5}{13}$ | B. | $-\frac{12}{13}$ | C. | $\frac{12}{13}$ | D. | $-\frac{5}{13}$ |
分析 利用任意角的三角函数的定义,求得cosθ的值.
解答 解:∵角θ的终边过点P(-12,5),则r=|OP|=13,
∴cosθ=$\frac{x}{r}$=$\frac{-12}{13}$=-$\frac{12}{13}$,
故选:B.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知函数f(x)=$\left\{\begin{array}{l}{-\sqrt{x},x>0}\\{(x-\frac{1}{x})^{4},x<0}\end{array}\right.$,则f(f(2))=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
18.如果点P(sin2θ,2cosθ)位于第三象限,那么角θ所在的象限是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
15.在△ABC中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b$,P在边BC上且BP=2PC,则$\overrightarrow{AP}$=( )
| A. | $\frac{4}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D. | $\frac{1}{3}\overrightarrow a+\frac{4}{3}\overrightarrow b$ |
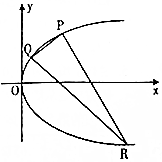 已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.
已知抛物线C:y2=4x,P为C上一点且纵坐标为2,Q,R是C上的两个动点,且PQ⊥PR.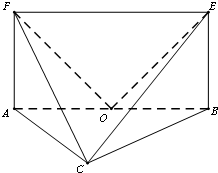 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.