题目内容
求函数y=
的值域．
| x2+2x+5 |
| x2+4x+4 |
考点：函数的值域
专题：函数的性质及应用
分析：由判别式法求函数的值域．
解答：
解：由y=
，得：
（y-1）x2+2（2y-1）x+4y-5=0，
∵x∈R
∴△=4（2y-1）2-4（y-1）（4y-5）≥0，
解得：y≤-
．
所以函数y=
的值域是（-∞，-
]
| x2+2x+5 |
| x2+4x+4 |
（y-1）x2+2（2y-1）x+4y-5=0，
∵x∈R
∴△=4（2y-1）2-4（y-1）（4y-5）≥0，
解得：y≤-
| 1 |
| 2 |
所以函数y=
| x2+2x+5 |
| x2+4x+4 |
| 1 |
| 2 |
点评：本题主要考查函数值域的求法，属于基础题．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
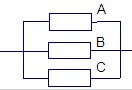如图，在一段线路中并联着3个自动控制的开关，只要其中有一个开关能够闭合，线路就正常工作，假在某段时间内每个开关能够闭合的概率是0.5，请你用树状图求出在这段时间内正常工作的概率．式子log3
的值为（ ）
| 1 |
| 81 |
| A、4 | ||
| B、-4 | ||
C、
| ||
D、-
|
已知0＜x＜1，a=2
，b=1+x，c=
，则其中最大的是（ ）
| x |
| 1 |
| 1-x |
| A、a | B、b | C、c | D、不确定 |