题目内容
设f(x)是定义在R上的奇函数，且对任意实数x都有f(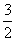
＋x)＝－f(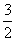－x)成立．
(1)证明y＝f(x)是周期函数，并指出其周期；
(2)若f(1)＝2，求f(2)＋f(3)的值；
(3)若g(x)＝x2＋ax＋3，且y＝|f(x)|·g(x)是偶函数，求实数a的值．
(1)证明略，3是其一个周期
(2)f(2)＋f(3)＝－2 (3)a＝0
练习册系列答案
相关题目
题目内容
设f(x)是定义在R上的奇函数，且对任意实数x都有f(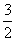＋x)＝－f(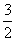－x)成立．
(1)证明y＝f(x)是周期函数，并指出其周期；
(2)若f(1)＝2，求f(2)＋f(3)的值；
(3)若g(x)＝x2＋ax＋3，且y＝|f(x)|·g(x)是偶函数，求实数a的值．
(1)证明略，3是其一个周期
(2)f(2)＋f(3)＝－2 (3)a＝0
；②y＝log
(a≠0)在同一坐标系中的图像可能是( )
的值．
若函数g(x)＝f(x)－k有两个不同的零点，则实数k的取值范围是________．