题目内容
6.已知$\overrightarrow{a}$=(2x,-1),$\overrightarrow{b}$=(-4,2),若$\overrightarrow{a}$$∥\overrightarrow{b}$,则x的值为( )| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 1 | D. | -1 |
分析 利用向量共线列出方程求解即可.
解答 解:$\overrightarrow{a}$=(2x,-1),$\overrightarrow{b}$=(-4,2),若$\overrightarrow{a}$$∥\overrightarrow{b}$,
可得4=4x,解得x=1.
故选:C.
点评 本题考查向量共线的充要条件的应用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.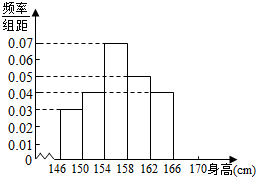 为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:
为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:
(Ⅰ)求出表中字母m,n所对应的数值;
(Ⅱ)在图中补全频率分布直方图;
(Ⅲ)根据频率分布直方图估计该校高一女生身高的中位数(保留两位小数)
 为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:
为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:| 组 别 | 频数 | 频率 |
| [146,150) | 6 | 0.12 |
| [150,154) | 8 | 0.16 |
| [154,158) | 14 | 0.28 |
| [158,162) | 10 | 0.20 |
| [162,166) | 8 | 0.16 |
| [166,170) | m | n |
| 合 计 | M | 1 |
(Ⅱ)在图中补全频率分布直方图;
(Ⅲ)根据频率分布直方图估计该校高一女生身高的中位数(保留两位小数)
14.已知集合A={x|y=lg(5-x)},B={y|y=lg(5-x)},则A∩B=( )
| A. | ∅? | B. | R | C. | (-∞,5) | D. | [0,5] |
11.若不等式x2+mx-m>0,的解集为R,则实数m的取值范围是( )
| A. | m<-4或m>0 | B. | m<0或m>4 | C. | -4<m<0 | D. | 0<m<4 |
18.若函数f(x)=$\left\{\begin{array}{l}{{5}^{-x},x∈(-1,0]}\\{{5}^{x},x∈[0,1]}\end{array}\right.$,则f(log54)=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{4}$ | D. | 4 |
15.已知集合M={0,1,2,3,4},N={x|1<log2(x+2)<2},则M∩N=( )
| A. | {0,1} | B. | {2,3} | C. | {1} | D. | {2,3,4} |
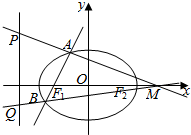 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.