题目内容
数列{an}中,a1=t,a2=t2,其中t>0且t≠1,x=
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
(Ⅰ)证明:数列{an+1-an}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设bn=anlogtan,数列{bn}的前n项和为Sn,求Sn.
| t |
(Ⅰ)证明:数列{an+1-an}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设bn=anlogtan,数列{bn}的前n项和为Sn,求Sn.
考点:数列的求和,等比数列的性质
专题:综合题,等差数列与等比数列
分析:(Ⅰ)求导函数,根据已知f′(
)=0,可得an+1-an=t(an-an-1),从而可以证明数列{an+1-an}是等比数列;
(Ⅱ)利用叠加法,可求数列{an}的通项公式;
(Ⅲ)由bn=anlogtan,求出数列{bn}的通项,利用错位相减法,可求前n项和为Sn.
| t |
(Ⅱ)利用叠加法,可求数列{an}的通项公式;
(Ⅲ)由bn=anlogtan,求出数列{bn}的通项,利用错位相减法,可求前n项和为Sn.
解答:
(Ⅰ)证明:f′(x)=3an-1x2-3[(t+1)an-an+1],
根据已知f′(
)=0,即tan-1-(t+1)an+an+1=0,
即an+1-an=t(an-an-1),…(2分)
∵t>0,t≠1,
∴a2-a1=t2-t=t(t-1)≠0,
∴数列{an+1-an}是以t(t-1)为首项,t为公比的等比数列.…(4分)
(Ⅱ)解:由于(Ⅰ)可知an+1-an=(t-1)tn.
所以an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(t-1)tn-1+(t-1)tn-1+…+(t-1)t+t
=(t-1)×
+t=tn.
∴数列{an}的通项公式an=tn. …(8分)
(Ⅲ)解:由(Ⅱ)知an=tn,
∴bn=anlogtan=ntn.…(9分)
∴Sn=1×t+2×t2+3×t3+…+ntn,
则tSn=1×t2+2×t3+…+(n-1)tn+ntn+1,…(10分)
∴(1-t)Sn=t+t2+t3+…+tn-ntn+1=
-ntn+1,…(13分)
∴Sn=
-
.…(14分)
根据已知f′(
| t |
即an+1-an=t(an-an-1),…(2分)
∵t>0,t≠1,
∴a2-a1=t2-t=t(t-1)≠0,
∴数列{an+1-an}是以t(t-1)为首项,t为公比的等比数列.…(4分)
(Ⅱ)解:由于(Ⅰ)可知an+1-an=(t-1)tn.
所以an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(t-1)tn-1+(t-1)tn-1+…+(t-1)t+t
=(t-1)×
| t(1-tn-1) |
| 1-t |
∴数列{an}的通项公式an=tn. …(8分)
(Ⅲ)解:由(Ⅱ)知an=tn,
∴bn=anlogtan=ntn.…(9分)
∴Sn=1×t+2×t2+3×t3+…+ntn,
则tSn=1×t2+2×t3+…+(n-1)tn+ntn+1,…(10分)
∴(1-t)Sn=t+t2+t3+…+tn-ntn+1=
| t(1-tn) |
| 1-t |
∴Sn=
| t-tn+1 |
| (1-t)2 |
| ntn+1 |
| 1-t |
点评:本题考查导数知识的运用,考查等比数列的证明,考查数列的通项与求和,确定数列的通项是关键.

练习册系列答案
相关题目
定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2]时,f(x)=
,若x∈[-2,0]时,f(x)≥
-
恒成立,则实数t的取值范围是( )
|
| t |
| 2 |
| 1 |
| t |
| A、[-2,0)∪(0,1) |
| B、[-2,0)∪[1,+∞) |
| C、[-2,1] |
| D、(-∞,-2]∪(0,1] |
 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.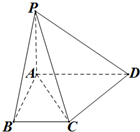 如图,直角梯形ABCD中,∠ABC=∠BAD=90°,
如图,直角梯形ABCD中,∠ABC=∠BAD=90°,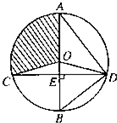 选修4-1几何证明选讲
选修4-1几何证明选讲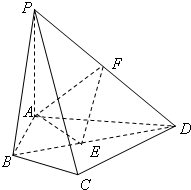 如图,四棱锥P-ABCD中,PA⊥面ABCD,E、F分别为BD、PD的中点,EA=EB=AB=1,PA=2.
如图,四棱锥P-ABCD中,PA⊥面ABCD,E、F分别为BD、PD的中点,EA=EB=AB=1,PA=2.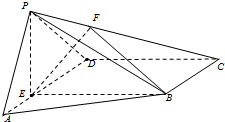 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.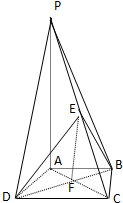 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=2,AD=4,DC=3,PA=5,E∈PC,AC∩BD=F.