题目内容
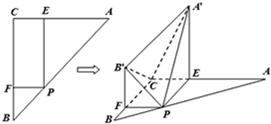 如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设
如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设| AP |
| PB |
(1)求证:B′C∥平面A′PE;
(2)是否存在正实数λ,使得二面角C-A′B′-P的大小为90°?若存在,求出λ的值;若不存在,请说明理由.
考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角,空间向量及应用
分析:(1)建立空间直角坐标系,求出平面A'PE的一个法向量
=(0,
,0),证明
•
=0,可得B'C∥平面A'PE;
(2)求出平面CA'B'、平面PA'B'的一个法向量,利用两个平面的法向量的夹角即可得出二面角.
| CE |
| a |
| λ+1 |
| CB′ |
| CE |
(2)求出平面CA'B'、平面PA'B'的一个法向量,利用两个平面的法向量的夹角即可得出二面角.
解答:
(1)证明:以C为原点,CB所在直线为x轴,CA所在直线为y轴,过C且垂直于平面ABC的直线为z轴,建立空间直角坐标系,如图,
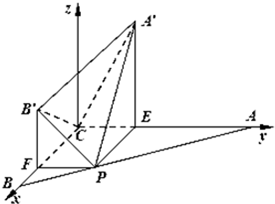
则C(0,0,0),A(0,a,0),B(a,0,0)设P(x,y,0),
由
=λ
⇒(x,y-a,0)=λ(a-x,-y,0)⇒x=
,y=
,
∴P(
,
,0),
从而E(0,
,0),F(
,0,0),
于是A′(0,
,
),B′(
,0,
),
平面A'PE的一个法向量为
=(0,
,0),
又
=(
,0,
),
•
=0,从而B'C∥平面A'PE.
(2)解:由(1)知有:
=(0,
,
),
=(
,-
,
),
=(0,
,-
).
设平面CA'B'的一个法向量为
=(x,y,-1),则
,
∴可得平面CA'B'的一个法向量
=(
,λ,-1),
同理可得平面PA'B'的一个法向量
=(1,1,1),
由
•
=0,即
+λ-1=0,
又λ>0,λ2-λ+1=0,由于△=-3<0,
∴不存在正实数λ,使得二面角 C-A'B'-P的大小为90°.

则C(0,0,0),A(0,a,0),B(a,0,0)设P(x,y,0),
由
| AP |
| PB |
| λa |
| λ+1 |
| a |
| λ+1 |
∴P(
| λa |
| λ+1 |
| a |
| λ+1 |
从而E(0,
| a |
| λ+1 |
| λa |
| λ+1 |
于是A′(0,
| a |
| λ+1 |
| λa |
| λ+1 |
| λa |
| λ+1 |
| a |
| λ+1 |
平面A'PE的一个法向量为
| CE |
| a |
| λ+1 |
又
| CB′ |
| λa |
| λ+1 |
| a |
| λ+1 |
| CB′ |
| CE |
(2)解:由(1)知有:
| CA′ |
| a |
| λ+1 |
| λa |
| λ+1 |
| A′B′ |
| λa |
| λ+1 |
| a |
| λ+1 |
| (1-λ)a |
| λ+1 |
| B′P |
| a |
| λ+1 |
| a |
| λ+1 |
设平面CA'B'的一个法向量为
| m |
|
∴可得平面CA'B'的一个法向量
| m |
| 1 |
| λ |
同理可得平面PA'B'的一个法向量
| n |
由
| m |
| n |
| 1 |
| λ |
又λ>0,λ2-λ+1=0,由于△=-3<0,
∴不存在正实数λ,使得二面角 C-A'B'-P的大小为90°.
点评:本题通过建立空间直角坐标系,利用两个平面的法向量的夹角得出二面角,证明线面平行是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
阅读如图所示的程序框图,则该算法的功能是( )
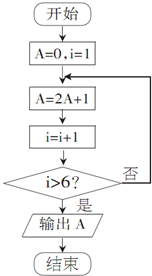

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前6项的和 |
| C、计算数列{2n-1}前5项的和 |
| D、计算数列{2n-1}前6项的和 |
 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.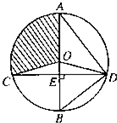 选修4-1几何证明选讲
选修4-1几何证明选讲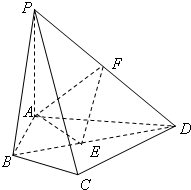 如图,四棱锥P-ABCD中,PA⊥面ABCD,E、F分别为BD、PD的中点,EA=EB=AB=1,PA=2.
如图,四棱锥P-ABCD中,PA⊥面ABCD,E、F分别为BD、PD的中点,EA=EB=AB=1,PA=2.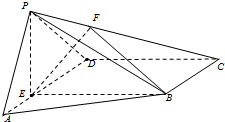 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD,AD∥BC,AD⊥CD,BC=ED=2AE,F为PC上一点,且CF=2FP.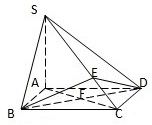 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.