题目内容
一个菱形边长与其内切圆的直径之比为k:1(k>1),则这个菱形的一个小于
的内角等于 .
| π |
| 2 |
考点:圆的切线的性质定理的证明
专题:直线与圆
分析:先做出图象,然后作辅助线将所求内角,内切圆直径转化到同一直角三角形中,求解即可.
解答:
解;由题意作菱形ABCD及其内切圆,则∠BAD为所求小于
的内角,设为θ,(0<θ<
),
又由题意知菱形边长与其内切圆的直径之比为k:1(k>1),不妨设菱形边长为k,内切圆直径为1,
过A作AE⊥CB交CB的延长线于点E,则AE长等于平行线AD与BC的距离,而在菱形ABCD中,内切圆直径长也等于平行线AD与BC的距离,则AE长等于内切圆直径长,AE=1,
∵∠ABE为△ABC一外角,∴∠ABE=∠BAC+∠BCA=∠BAD=θ,
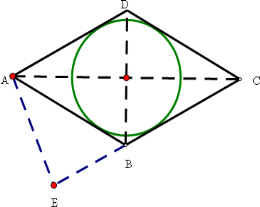 在Rt△AEB中,AE=1,AB=k,
在Rt△AEB中,AE=1,AB=k,
sinθ=
,
cosθ=
=
,
tanθ=
,
θ=arctan
.
| π |
| 2 |
| π |
| 2 |
又由题意知菱形边长与其内切圆的直径之比为k:1(k>1),不妨设菱形边长为k,内切圆直径为1,
过A作AE⊥CB交CB的延长线于点E,则AE长等于平行线AD与BC的距离,而在菱形ABCD中,内切圆直径长也等于平行线AD与BC的距离,则AE长等于内切圆直径长,AE=1,
∵∠ABE为△ABC一外角,∴∠ABE=∠BAC+∠BCA=∠BAD=θ,
 在Rt△AEB中,AE=1,AB=k,
在Rt△AEB中,AE=1,AB=k,sinθ=
| 1 |
| k |
cosθ=
1-(
|
|
tanθ=
|
θ=arctan
|
点评:做出图形,利用数形结合将条件直观显示出来,有助于我们解题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
等比数列{an}中,a3=7,前3项之和s3=21,则公比q的值是( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
sin(π+α)=( )
| A、cosα | B、-cosα |
| C、sinα | D、-sinα |
已知M(-c,0),N(c,0),若|PM|-|PN|=c(c>0),则动点P的轨迹是( )
| A、双曲线的左支 |
| B、双曲线的右支 |
| C、以N为端点的射线 |
| D、线段MN |
