题目内容
15．直线l：x-ty-1=0将圆（x-3）2+（y-3）2=4的弧长恰好分成1：2两部分，则此时的弦长为（ ）| A． | 2 | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | 4 |
分析 由已知得弦AB所对圆心角∠AOB=120°，由此能求出弦长．
解答 
解：∵直线l：x-ty-1=0将圆（x-3）2+（y-3）2=4的弧长恰好分成1：2两部分，如图，
∴劣$\widehat{AB}$=120°，∴∠AOB=120°，
取AB中点C，连结OC，则∠BOC=60°，∠OBC=30°，OC⊥AB，
∴OC=$\frac{1}{2}OB=1$，
∴AB=2BC=2$\sqrt{4-1}$=2$\sqrt{3}$．
故选：C．
点评 本题考查弦长的求法，是基础题，解题时要认真审题，注意直线与圆的位置关系的合理运用．
练习册系列答案
相关题目
5．在某次测量中得到的A样本数据如下：72，74，74，76，76，76，77，77，77，77．若B样本数据恰好是A样本数据每个都减2后所得数据，则A，B两样本的下列数字特征对应相同的是（ ）
| A． | 众数 | B． | 平均数 | C． | 中位数 | D． | 标准差 |
（1）如图（1）所示，在北纬30°圈上两地A，B的经度差为锐角θ，若sinθ=$\frac{2\sqrt{2}}{3}$，求A，B两地间的球面距离（地球半径为R）．
3．
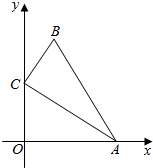如图，在△ABC中，∠ACB=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点O的最大距离是（ ）
如图，在△ABC中，∠ACB=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点O的最大距离是（ ）| A． | 3 | B． | $\sqrt{6}$ | C． | $1+\sqrt{2}$ | D． | $\sqrt{5}$ |