题目内容
12．函数f（x）=log2x在区间$[{\frac{1}{2}，2}]$上的最小值是（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 先分析函数f（x）=log2x的单调性，进而可得函数f（x）=log2x在区间$[\frac{1}{2}，2]$上的最小值．
解答 解：∵函数f（x）=log2x在区间$[\frac{1}{2}，2]$上为增函数，
∴当x=$\frac{1}{2}$时，函数f（x）取最小值-1，
故选：A．
点评 本题考查的知识点是对数函数的图象和性质，其中熟练掌握对数函数的单调性与底数的关系是解答的关键．
练习册系列答案
相关题目
（1）如图（1）所示，在北纬30°圈上两地A，B的经度差为锐角θ，若sinθ=$\frac{2\sqrt{2}}{3}$，求A，B两地间的球面距离（地球半径为R）．
3．
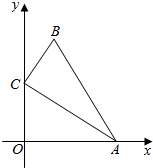如图，在△ABC中，∠ACB=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点O的最大距离是（ ）
如图，在△ABC中，∠ACB=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点O的最大距离是（ ）| A． | 3 | B． | $\sqrt{6}$ | C． | $1+\sqrt{2}$ | D． | $\sqrt{5}$ |
7．设实数数列{an}，{bn}分别为等差数列与等比数列，且a1=b1=4，a4=b4=1，则以下结论正确的是（ ）
| A． | a1＞b2 | B． | a3＜b3 | C． | a5＞b5 | D． | a6＞b6 |
17．命题“若a2+b2=0，则a=0且b=0”的逆否命题是（ ）
| A． | 若a≠0或b≠0，则a2+b2≠0 | B． | 若a2+b2≠0，则a≠0且b≠0 | ||
| C． | 若a2+b2≠0，则a≠0或b≠0 | D． | 若a=0且b=0，则a2+b2≠0 |
如图是甲、乙两名篮球运动员2013年赛季每场比赛得分的茎叶图，则甲中位数和乙的平均数之和为$\frac{381}{7}$．
1．若直线l1：ax+3y=0与l2：2x+（a+1）y+1=0互相平行，则a的值是（ ）
| A． | -3或2 | B． | 2 | C． | 3 | D． | -3 |
2．
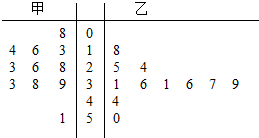如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图，其中茎为十位数，叶为个位数，甲、乙两人得分的中位数为X甲、X乙，则下列判断正确的是（ ）
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图，其中茎为十位数，叶为个位数，甲、乙两人得分的中位数为X甲、X乙，则下列判断正确的是（ ）| A． | X乙-X甲=5，甲比乙得分稳定 | B． | X乙-X甲=5，乙比甲得分稳定 | ||
| C． | X乙-X甲=10，甲比乙得分稳定 | D． | X乙-X甲=10，乙比甲得分稳定 |