题目内容
13．为了研究雾霾天气的治理，某课题组对部分城市进行空气质量调查，按地域特点把这些城市分成甲、乙、丙三组，已知三组城市的个数分别为4，y，z，依次构成等差数列，且4，y，z+4成等比数列，若用分层抽样抽取6个城市，则乙组中应抽取的城市个数为3．分析 利用三组城市的个数分别为4，y，z，依次构成等差数列，且4，y，z+4成等比数列，求出y，z，根据分层抽样的定义建立比例关系即可．
解答 解：∵三组城市的个数分别为4，y，z，依次构成等差数列，且4，y，z+4成等比数列，
∴$\left\{\begin{array}{l}{4+z=2y}\\{{y}^{2}=4（z+4）}\end{array}\right.$，
∴y=12，z=8，
若用分层抽样抽取6个城市，则乙组中应该抽取的城市数为$\frac{12}{24}×6$=3，
故答案为：3
点评 本题主要考查等差数列、等比数列的性质，考查分层抽样的应用，属于中档题．
练习册系列答案
相关题目
（1）如图（1）所示，在北纬30°圈上两地A，B的经度差为锐角θ，若sinθ=$\frac{2\sqrt{2}}{3}$，求A，B两地间的球面距离（地球半径为R）．
1．集合A={x|0＜x≤3，x∈Z}的真子集的个数是（ ）
| A． | 8 | B． | 7 | C． | 6 | D． | 3 |
8．已知函数y=f（x）的图象经过点P（1，-2），则函数y=-f（-x）的图象必过点（ ）
| A． | （-1，2） | B． | （1，2） | C． | （-1，-2） | D． | （-2，1） |
18．已知函数f（x）满足f（4+x）=f（-x）．当x1，x2∈（-∞，2）时，$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＞0；当x1，x2∈（2，+∞）时，$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜0．若x1＜x2，且x1+x2＞4，则f（x1），f（x2）的大小关系是（ ）
| A． | f（x1）＜f（x2） | B． | f（x1）＞f（x2） | C． | f（x1）=f（x2） | D． | 不确定 |
3．
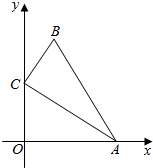如图，在△ABC中，∠ACB=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点O的最大距离是（ ）
如图，在△ABC中，∠ACB=90°，AC=2，BC=1，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点O的最大距离是（ ）| A． | 3 | B． | $\sqrt{6}$ | C． | $1+\sqrt{2}$ | D． | $\sqrt{5}$ |
1．若直线l1：ax+3y=0与l2：2x+（a+1）y+1=0互相平行，则a的值是（ ）
| A． | -3或2 | B． | 2 | C． | 3 | D． | -3 |