题目内容
函数y=
的定义域是 .
| 1 |
| log3(3x-2) |
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:根据对数函数的真数必须大于0,同时分式分母不为0,列出不等式组,解出即可.
解答:
解:要使函数y=
有意义,
则3x-2>0,且log3(3x-2)≠0,
即x>
且3x-2≠1,
即x>
且x≠1.
则定义域为{x|x>
且x≠1}.
故答案为:{x|x>
且x≠1}.
| 1 |
| log3(3x-2) |
则3x-2>0,且log3(3x-2)≠0,
即x>
| 2 |
| 3 |
即x>
| 2 |
| 3 |
则定义域为{x|x>
| 2 |
| 3 |
故答案为:{x|x>
| 2 |
| 3 |
点评:本题考查函数的定义域的求法,注意对数函数的真数必须大于0,同时考虑分母不为0,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将87化成二进制数为( )
| A、1010111(2) |
| B、1010110(2) |
| C、1110101(2) |
| D、1010101(2) |
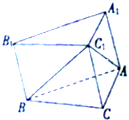 如图,在斜三棱柱ABC-A1B1C1的底面△ABC中,∠BAC=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( )
如图,在斜三棱柱ABC-A1B1C1的底面△ABC中,∠BAC=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( )| A、直线AC上 |
| B、直线AB上 |
| C、直线BC上 |
| D、△ABC内部 |