题目内容
16．
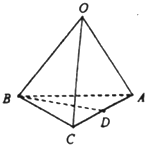如图，在三棱锥O-ABC中，点D是棱AC的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则$\overrightarrow{BD}$等于（ ）| A． | -$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | B． | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ | C． | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D． | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
分析 利用向量的三角形法则，表示所求向量，化简求解即可．
解答 解：由题意在三棱锥O-ABC中，点D是棱AC的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，
可知：$\overrightarrow{BD}$=$\overrightarrow{BO}$+$\overrightarrow{OD}$，$\overrightarrow{BO}$=$-\overrightarrow{b}$，
$\overrightarrow{OD}$=$\frac{1}{2}\overrightarrow{OA}$$+\frac{1}{2}\overrightarrow{OC}$=$\frac{1}{2}\overrightarrow{a}$$+\frac{1}{2}$$\overrightarrow{c}$，
$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$．
故选：C．
点评 本题考查向量的三角形法则，空间向量与平面向量的转化，是基础题．
练习册系列答案
相关题目
7．某学生记忆导数公式如下，其中错误的一个是（ ）
| A． | （${\frac{1}{x}}$）′=-$\frac{1}{x^2}$ | B． | （ax）=axlna | C． | （lnx）′=$\frac{1}{x}$ | D． | （sinx）′=-cosx |
4．函数y=x2-（4a+1）x+3a2+3a的图象与x轴交于A、B两点，若两点间的距离等于2，则a的值为（ ）
| A． | $\frac{3}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{3}{2}$或-$\frac{1}{2}$ | D． | $\frac{3}{2}$或-$\frac{2}{3}$ |
1．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左顶点为A（-1，0），右焦点为F2（$\sqrt{3}$，0），则双曲线的渐近线方程为（ ）
| A． | y=±$\sqrt{2}$x | B． | y=±2x | C． | y=±$\frac{\sqrt{2}}{2}$x | D． | y=±$\frac{1}{2}$x |
8．下列命题中的假命题是（ ）
| A． | ?x∈R，lgx=0 | B． | ?x∈R，x3＞0 | C． | ?x∈R，tanx=1 | D． | ?x∈R，2x＞0 |
7．已知e=2.71828…，设函数f（x）=$\frac{1}{2}$x2-bx+alnx存在极大值点x0，且对于b的任意可能取值，恒有极大值f（x0）＜0，则下列结论中正确的是（ ）
| A． | 存在x0=$\sqrt{a}$，使得f（x0）＜-$\frac{1}{e}$ | B． | 存在x0=$\sqrt{a}$，使得f（x0）＞-e | ||
| C． | a的最大值为e3 | D． | 0＜a＜e3 |