题目内容
1.已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数,当x=1时f(x)取得极值-2.(1)求a,c,d的值,并求f(x)的极大值;
(2)证明对任意x1,x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.
分析 (1)由奇函数的定义利用待定系数法求得d,再由x=1时f(x)取得极值-2.解得a,c从而确定函数,再利用导数求单调区间和极大值.
(2)由(1)知,f(x)=x3-3x(x∈[-1,1])是减函数,从而确定|f(x1)-f(x2)|最小值,证明即可.
解答 解:(1)由奇函数的定义,应有f(-x)=-f(x),x∈R
即-ax3-cx+d=-ax3-cx-d∴d=0,
因此,f(x)=ax3+cxf'(x)=3ax2+c,
由条件f(1)=-2为f(x)的极值,必有f'(1)=0,
故 $\left\{\begin{array}{l}{a+c=-2}\\{3a+c=0}\end{array}\right.$,解得a=1,c=-3,
因此,f(x)=x3-3x,f'(x)=3x2-3=3(x+1)(x-1)f'(-1)=f'(1)=0,
当x∈(-∞,-1)时,f'(x)>0,故f(x)在单调区间(-∞,-1)上是增函数,
当x∈(-1,1)时,f'(x)<0,故f(x)在单调区间(-1,1)上是减函数,
当x∈(1,+∞)时,f'(x)>0,故f(x)在单调区间(1,+∞)上是增函数,
所以,f(x)在x=-1处取得极大值,极大值为f(-1)=2;
(2)由(1)知,f(x)=x3-3x(x∈[-1,1])是减函数,
且f(x)在[-1,1]上的最大值M=f(-1)=2,
f(x)在[-1,1]上的最小值m=f(1)=-2
所以,对任意的x1,x2∈(-1,1),
恒有|f(x1)-f(x2)|<M-m=2-(-2)=4.
点评 本小题主要考查函数的单调性及奇偶性,考查运用导数研究函数单调性及极值等基础知识,考查综合分析和解决问题的能力.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
8.下列命题中的假命题是( )
| A. | ?x∈R,lgx=0 | B. | ?x∈R,x3>0 | C. | ?x∈R,tanx=1 | D. | ?x∈R,2x>0 |
10.若直线l1:mx+y-1=0,l2:4x+my+m-4=0,则“m=2”是“直线l1⊥l2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
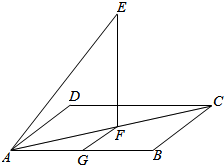 如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题:
如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题: