题目内容
7.已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点$M(1,\frac{{2\sqrt{3}}}{3})$,离心率为$\frac{{\sqrt{3}}}{3}$.(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若A1,A2是椭圆E的左右顶点,过点A2作直线l与x轴垂直,点P是椭圆E上的任意一点(不同于椭圆E的四个顶点),联结PA;交直线l与点B,点Q为线段A1B的中点,求证:直线PQ与椭圆E只有一个公共点.
分析 (Ⅰ)利用椭圆的离心率公式,将M代入椭圆方程,即可求得a和b的值,即可求得椭圆E的标准方程;
(Ⅱ)利用点斜方程,求得直线PA1的方程,求得B的中点,利用中点坐标公式求得Q坐标,求得直线PQ的斜率,直线PQ方程为$y-{y_0}=-\frac{{2{x_0}}}{{3{y_0}}}(x-{x_0})$,代入椭圆方程,由△=0,则直线PQ与椭圆E相切,即直线PQ与椭圆E只有一个公共点.
解答 解:(Ⅰ)由题意可得:$\left\{\begin{array}{l}e=\frac{c}{a}=\frac{{\sqrt{3}}}{3}\\ \frac{1}{a^2}+\frac{4}{{3{b^2}}}=1\\{a^2}={b^2}+{c^2}\end{array}\right.$,解得:a=$\sqrt{3}$,b=$\sqrt{2}$,c=1,
∴椭圆E的标准方程为$\frac{x^2}{3}+\frac{y^2}{2}=1$.
(Ⅱ)证明:设P(x0,y0)(x0≠0且${x_0}≠±\sqrt{3})$,直线PA1的方程为:$y=\frac{y_0}{{{x_0}+\sqrt{3}}}(x+\sqrt{3})$,
令$x=\sqrt{3}$得$B=(\sqrt{3},\frac{{2\sqrt{3}{y_0}}}{{{x_0}+\sqrt{3}}})$,则线段A2B的中点$Q(\sqrt{3},\frac{{\sqrt{3}{y_0}}}{{{x_0}+\sqrt{3}}})$,
则直线PQ的斜率${K_{PQ}}=\frac{{{y_0}-\frac{{\sqrt{3}{y_0}}}{{{x_0}+\sqrt{3}}}}}{{{x_0}-\sqrt{3}}}=\frac{{{x_0}{y_0}}}{x_0^2-3}$,①
∵P是椭圆E上的点,
∴$x_0^2=3(1-\frac{y_0^2}{2})$,代入①式,得${k_{PQ}}=-\frac{{2{x_0}}}{{3{y_0}}}$,
∴直线PQ方程为$y-{y_0}=-\frac{{2{x_0}}}{{3{y_0}}}(x-{x_0})$,
联立$\left\{\begin{array}{l}y-{y_0}=-\frac{{2{x_0}}}{{3{y_0}}}(x-{x_0})\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.$,
又∵$2{x_0}^2+3{y_0}^2=6$,整理得${x^2}-2{x_0}x+{x_0}^2=0$,
∵△=0
∴直线PQ与椭圆E相切,即直线PQ与椭圆E只有一个公共点.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查直线的斜率公式,中点坐标公式,考查计算能力,属于中档题.

| A. | (0,4) | B. | (4,+∞) | C. | {1,2,3} | D. | {1,2,3,4} |
| A. | $\frac{1}{64}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{8}$ |
| A. | -1 | B. | 1 | C. | 0 | D. | $\frac{1}{2}$ |
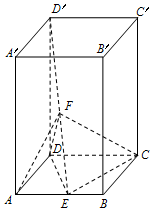 如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.
如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.