题目内容
10.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上任意一点M与左右顶点A1、A2连线的斜率之积为$\frac{3}{4}$,则双曲线的离心率为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\frac{5}{3}$ |
分析 设出M的坐标,利用已知条件,转化求解双曲线的离心率即可.
解答 解:设M(m,n),由题意可得:$\frac{{m}^{2}}{{a}^{2}}-\frac{{n}^{2}}{{b}^{2}}=1$,${m}^{2}=\frac{{a}^{2}({b}^{2}+{n}^{2})}{{b}^{2}}$,
并且:$\frac{n}{m-a}•\frac{n}{m+a}=\frac{3}{4}$,
可得$\frac{{n}^{2}}{{m}^{2}-{a}^{2}}$=$\frac{3}{4}$,
所以$\frac{{n}^{2}}{\frac{{a}^{2}({b}^{2}+{n}^{2})}{{b}^{2}}-{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$=$\frac{3}{4}$,∴$\frac{{c}^{2}}{{a}^{2}}$=$\frac{7}{4}$,
e=$\frac{\sqrt{7}}{2}$.
故选:C.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
20.设a∈R,若复数z=$\frac{a-i}{3+i}$(i是虚数单位)的实部为$\frac{1}{2}$,则a的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | -2 | D. | 2 |
1.在2013年至2016年期间,甲每年6月1日都到银行存入m元的一年定期储蓄,若年利率为q保持不变,且每年到期的存款本息自动转为新的一年定期,到2017年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
| A. | m(1+q)4元 | B. | m(1+q)5元 | C. | $\frac{m[(1+q)^{4}-(1+q)]}{q}$元 | D. | $\frac{m[(1+q)^{5}-(1+q)]}{q}$元 |
18.锐角三角形ABC的三边长a,b,c成等差数列,且a2+b2+c2=21,则实数b的取值范围是( )
| A. | $({\sqrt{6},\sqrt{7}}]$ | B. | $({0,\sqrt{7}}]$ | C. | $({\frac{{2\sqrt{42}}}{5},\sqrt{7}}]$ | D. | (6,7] |
5.设i是虚数单位,复数z满足z•(1+$\sqrt{2}$i)=-$\sqrt{2}$i,则复数z的虚部等于( )
| A. | -$\frac{\sqrt{2}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | -$\frac{2}{3}$ |
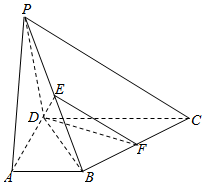 在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.
在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.