题目内容
若函数f(x)=2cos2x+asinx-1在区间(
,
)是减函数,则a的取值范围是 .
| π |
| 6 |
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:首先,求解导数,然后将问题转化为:f′(x)=-2sin2x+acosx≤0在区间(
,
)上恒成立问题,然后,分离参数求解其范围.
| π |
| 6 |
| π |
| 2 |
解答:
解:∵函数f(x)=2cos2x+asinx-1,
∴f′(x)=2sin2x+acosx
∴f′(x)=-2sin2x+acosx≤0在区间(
,
)上恒成立,
∴a≤
=4sinx,
∵x∈(
,
)
∴sinx∈(
,1),
∴4sinx∈(2,4),
∴a≤2,
故答案为:(-∞,2].
∴f′(x)=2sin2x+acosx
∴f′(x)=-2sin2x+acosx≤0在区间(
| π |
| 6 |
| π |
| 2 |
∴a≤
| 2sin2x |
| cosx |
∵x∈(
| π |
| 6 |
| π |
| 2 |
∴sinx∈(
| 1 |
| 2 |
∴4sinx∈(2,4),
∴a≤2,
故答案为:(-∞,2].
点评:本题重点考查了三角函数的图象与性质、导数的应用、函数的单调性与导数等知识,属于中档题,解题关键是注意恒成立问题的处理思路和方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知{an},{bn}均为等差数列,且a2=8,a6=16,b2=4,b6=a6,则由{an},{bn}的公共项组成的新数列{cn}的通项公式cn等于( )
| A、3n+4 | B、6n+2 |
| C、6n+4 | D、2n+2 |
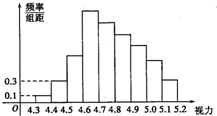 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,视力在4.6到5.0之间的学生数为a,则a的值为( )
为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,视力在4.6到5.0之间的学生数为a,则a的值为( )