题目内容
求下列代数式的值:
(1)已知sin(3π+α)=
,求
+
(2)已知tanα=2,求
sin2α+
sin2α+
cos2α.
(1)已知sin(3π+α)=
| 1 |
| 4 |
| cos(π+α) |
| cosα•[cos(π+α)-1] |
| cos(α-2π) |
| cos(α+2π)•cos(α+π)+cos(-α) |
(2)已知tanα=2,求
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)易求sinα=-
,利用诱导公式将所求关系式化简为
,将sinα=-
代入即可求得其值;
(2)将所求关系式转化为
,再将tanα=2代入即可求得答案.
| 1 |
| 4 |
| 2 |
| sin2α |
| 1 |
| 4 |
(2)将所求关系式转化为
| ||||||
| tan2α+1 |
解答:
解:(1)因为sin(3π+α)=
,
所以sinα=-
,---------------(2分)
又
+
=
+
=
+
-----------------(4分)
=
=32-----------------(6分)
(2)因为
sin2α+
sin2α+
cos2α
=
=
.---------------------(10分)
将tanα=2代入,可得
=
-------------------(12分)
| 1 |
| 4 |
所以sinα=-
| 1 |
| 4 |
又
| cos(π+α) |
| cosα•[cos(π+α)-1] |
| cos(α-2π) |
| cos(α+2π)•cos(α+π)+cos(-α) |
=
| -cosα |
| cosα•(-cosα-1) |
| cosα |
| cosα•(-cosα)+cos(-α) |
=
| 1 |
| cosα+1 |
| 1 |
| -cosα+1 |
=
| 2 |
| sin2α |
=32-----------------(6分)
(2)因为
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| ||||||
| sin2α+cos2α |
=
| ||||||
| tan2α+1 |
将tanα=2代入,可得
| ||||||
| 22+1 |
| 13 |
| 30 |
点评:本题考查运用诱导公式化简求值,考查同角三角函数基本关系的运用,属于中档题.

练习册系列答案
相关题目
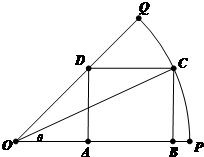 已知OPQ是半径为1,圆心角为
已知OPQ是半径为1,圆心角为 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2