题目内容
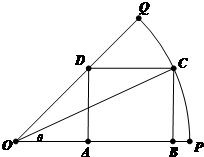 已知OPQ是半径为1,圆心角为
已知OPQ是半径为1,圆心角为| π |
| 4 |
(1)求当角θ取何值时,矩形ABCD的面积最大?并求出这个最大值.
(2)当矩形ABCD的面积为
| ||
| 4 |
考点:三角函数中的恒等变换应用,弧度制的应用
专题:三角函数的求值
分析:(1)在Rt△OBC中:OB=cosθ,BC=sinθ,利用直角三角形中的边角关系求出OA,可得AB,可得矩形ABCD的面积S=AB•BC=(cosθ-sinθ)sinθ,再利用三角恒等变换化为
sin(2θ+
)-
,利用正弦函数的定义域和值域求得面积S的最大值.
(2)当S=
sin(2θ+
)-
=
时,求得sin(2θ+
)=
,再结合θ的范围,求出θ的值.
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
(2)当S=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| π |
| 4 |
| ||
| 2 |
解答:
解:(1)在Rt△OBC中:OB=cosθ,BC=sinθ,
在Rt△OAD中:
=tan
=1,∴OA=AD=BC=sinθ,AB=OB-OA=cosθ-sinθ,
所以矩形ABCD的面积S=AB•BC=(cosθ-sinθ)sinθ
=cosθsinθ-sin2θ=
sin2θ-
=
(sin2θ+cos2θ)-
=
(
sin2θ+
cos2θ)-
=
sin(2θ+
)-
,
由0<θ<
,得
<2θ+
<
,
所以当2θ+
=
,即θ=
时,Smax=
-
.
(2)当S=
sin(2θ+
)-
=
时,即sin(2θ+
)=
,
又因为
<2θ+
<
,所以2θ+
=
,即θ=
.
在Rt△OAD中:
| AD |
| OA |
| π |
| 4 |
所以矩形ABCD的面积S=AB•BC=(cosθ-sinθ)sinθ
=cosθsinθ-sin2θ=
| 1 |
| 2 |
| 1-cos2θ |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
由0<θ<
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
所以当2θ+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| ||
| 2 |
| 1 |
| 2 |
(2)当S=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| π |
| 4 |
| ||
| 2 |
又因为
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 2π |
| 3 |
| 5π |
| 24 |
点评:本题主要考查三角函数的恒等变换,直角三角形中的边角关系,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
 如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥BC,E,F分别是A1B,AC1的中点. 如图在边长为a的正方形ABCD中,E、F分别为边BC、CD中点,设
如图在边长为a的正方形ABCD中,E、F分别为边BC、CD中点,设 (文科)已知如图,在三棱锥P-ABC中,顶点P在底面的投影H是△ABC的垂心.
(文科)已知如图,在三棱锥P-ABC中,顶点P在底面的投影H是△ABC的垂心.