题目内容
19.在复平面内,复数z=i(2-i),则|z|=$\sqrt{5}$.分析 利用复数的运算法则、模的计算公式即可得出.
解答 解:复数z=i(2-i)=1+2i,
∴|z|=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了复数的运算法则、模的计算公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.F1,F2分别是双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右焦点,过F2的直线l与双曲线的左右两支分别交于A,B两点,若△ABF1是等边三角形,则该双曲线的虚轴长为( )
| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 4$\sqrt{2}$ |
7.已知a为函数f(x)=x3-3x的极小值点,则a=( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
4. 如图在一个60° 的二面角的棱上有两个点A,B,线段分别AC、BD在这个二面 角的两个面内,并且都垂直于棱AB,且AB=AC=a,BD=2a,则CD 的长为( )
如图在一个60° 的二面角的棱上有两个点A,B,线段分别AC、BD在这个二面 角的两个面内,并且都垂直于棱AB,且AB=AC=a,BD=2a,则CD 的长为( )
 如图在一个60° 的二面角的棱上有两个点A,B,线段分别AC、BD在这个二面 角的两个面内,并且都垂直于棱AB,且AB=AC=a,BD=2a,则CD 的长为( )
如图在一个60° 的二面角的棱上有两个点A,B,线段分别AC、BD在这个二面 角的两个面内,并且都垂直于棱AB,且AB=AC=a,BD=2a,则CD 的长为( )| A. | 2a | B. | $\sqrt{5}$a | C. | a | D. | $\sqrt{3}$a |
11.各项均为正数的等比数列{an}的前n项和为Sn,若S4=10,S12=130,则S8=( )
| A. | -30 | B. | 40 | C. | 40或-30 | D. | 40或-50 |
9.设x,y满足约束条件$\left\{\begin{array}{l}8x-y-4≤0\\ x+y+1≥0\\ y-4x≤0\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为2,则$\frac{1}{a}+\frac{1}{b}$的最小值为( )
| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 9 |
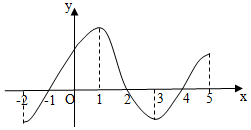 如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).
如图是函数y=f(x)的导数的图象,则正确的判断是(2)(4).