题目内容
13.(理科)已知数列{an}的各项均为正数,前n项和为Sn,且Sn=$\frac{{{a_n}({a_n}+1)}}{2}$,n∈N*.(1)求证:数列{an}是等差数列;
(2)设bn=$\frac{1}{{{a_n}^2}}$,Tn=b1+b2+…+bn,求证:$1≤{T_n}<\frac{7}{4}$.
分析 (1)利用递推关系、等差数列的定义即可证明;
(2)利用数列的单调性与“裂项求和”即可证明.
解答 (1)证明:∵Sn=$\frac{{{a_n}({a_n}+1)}}{2}$,n∈N*.
∴当n=1时,a1=S1=$\frac{{a}_{1}({a}_{1}+1)}{2}$ (an>0),∴a1=1.
当n≥2时,由an=Sn-Sn-1=$\frac{{a}_{n}({a}_{n}+1)}{2}$-$\frac{{a}_{n-1}({a}_{n-1}+1)}{2}$.
化为(an+an-1)(an-an-1-1)=0,
∵an+an-1>0,
∴an-an-1=1(n≥2).
∴数列{an}是以1为首项,以1为公差的等差数列.
(2)证明:bn=${a_n}^2$=$\frac{1}{{n}^{2}}$.
当n=1时,b1=1<$\frac{7}{4}$;
当n=2时,b1+b2=1+$\frac{1}{4}$=$\frac{5}{4}$<$\frac{7}{4}$;
当n≥3时,bn=$\frac{1}{{n}^{2}}$<$\frac{1}{(n-1)n}$=$\frac{1}{n-1}$-$\frac{1}{n}$,
此时Tn=1+$\frac{1}{4}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{4}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+$\frac{1}{4}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n-1)}$=$\frac{5}{4}$+$\frac{1}{2}$-$\frac{1}{n}$=$\frac{7}{4}$-$\frac{1}{n}$<$\frac{7}{4}$,
∴Tn<$\frac{7}{4}$.
又Tn≥T1=1,
∴$1≤{T_n}<\frac{7}{4}$.
点评 本题考查了递推关系、等差数列的定义、数列的单调性与“裂项求和”、不等式的性质,考查了推理能力与计算能力,属于中档题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | (0,4] | B. | [0,2)U(2,4) | C. | (0,2)U(2,4) | D. | [0,2)U(2,4] |
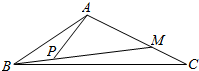 如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )| A. | -2 | B. | 2 | C. | $\frac{2}{3}$ | D. | $-\frac{11}{3}$ |
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
| A. | (-1,0) | B. | (0,3) | C. | (-1,1) | D. | (0,1) |