题目内容
将函数y=sin（2x+
）图象上的所有点向左平移
个单位，得到的图象的函数解析式是（ ）
| π |
| 4 |
| π |
| 4 |
A、y=sin（2x+
| ||
B、y=sin（2x+
| ||
C、y=sin（2x-
| ||
| D、y=sin2x |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：根据三角函数的平移关系即可得到结论．
解答：
解：将函数y=sin（2x+
）的图象向左平移
个单位长度，
得到y=sin[2（x+
）+
]=sin（2x+
+
）=sin（2x+
），
故选：A．
| π |
| 4 |
| π |
| 4 |
得到y=sin[2（x+
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
故选：A．
点评：本题主要考查三角函数解析式的求解，根据三角函数的图象变换关系是解决本题的关键．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
已知{an}为等比数列，Sn是它的前n项和．若a2•a3=2a1，且a4与2a7的等差中项为
，则S5=（ ）
| 5 |
| 4 |
| A、31 | B、32 | C、33 | D、34 |
在锐角△ABC中，角A，B，C所对的边长分别为a，b，c，若b=7，c=3，cosC=
，则B等于（ ）
| 13 |
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=sin（
-2x）cos（
+2x）的周期及单调递减区间分别是（ ）
| π |
| 6 |
| π |
| 6 |
A、
| ||||||||||
B、π（
| ||||||||||
C、
| ||||||||||
D、
|
如图，在同一直角坐标系中，正确表示直线y=ax与y=x+a的是（ ）
A、 |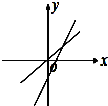
B、 |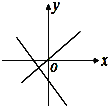
C、 |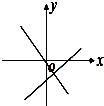
D、 |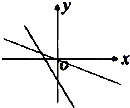
下列各式中正确的是（ ）
A、sin2
| ||||||
B、若a∈（0，2π），则一定有tana=
| ||||||
C、sin
| ||||||
D、sina=tana•cosa（a≠kπ+
|