题目内容
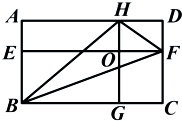
如图所示：在矩形ABCD中，EF∥BC，HG∥AB，且矩形AEOH，HOFD，OGCF的面积分别为9，4，7，则△HBF的面积 ．
考点：平行线分线段成比例定理
专题：立体几何
分析：据矩形的面积=长×宽，可得宽一定时，矩形的面积与长成正比例，所以设矩形EBGO的面积是x，则可得出比例式为：x：7=9：4，据此即可求出矩形EBGO的面积是15.75，则中间的△HBF的面积就等于这个大矩形ABCD的面积，减去矩形ABGH的一半，减去矩形HOFD的一半，再减去矩形BCFE的一半，据此代入数据计算即可解答问题
解答：
解：根据题干分析可得设矩形EBGO的面积是x，则可得出比例式为：
x：7=9：4
4x=63
x=15.75
即矩形EBGO的面积是15.75，
大矩形ABCD的面积是：9+4+7+15.75=35.75，
所以△HBF的面积是：35.75-（9+15.75）÷2-4÷2-（15.75+7）÷2
=35.75-12.375-2-11.375
=10
故答案为：10
x：7=9：4
4x=63
x=15.75
即矩形EBGO的面积是15.75，
大矩形ABCD的面积是：9+4+7+15.75=35.75，
所以△HBF的面积是：35.75-（9+15.75）÷2-4÷2-（15.75+7）÷2
=35.75-12.375-2-11.375
=10
故答案为：10
点评：本题考查了平面几何图形面积的求法；解答此题的关键是根据矩形的宽一定时，面积与长成正比例的性质，求出矩形EBGO的面积．
练习册系列答案
相关题目
已知m，n是两条不重合的直线，α，β，γ是三个两两不重合的平面，给出下列四个命题
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
| A、①和② | B、①和③ |
| C、①和④ | D、③和④ |
数列1，x，x2，…xn-1的和等于（ ）
| A、1 | ||
| B、n | ||
C、
| ||
| D、以上均不正确 |
已知{an}是等差数列，若a2+a4=6，a5=5，数列{bn}满足bn=anan+1，则
+
+…+
等于（ ）
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
A、
| ||
B、
| ||
C、
| ||
D、
|
将函数y=sin（2x+
）图象上的所有点向左平移
个单位，得到的图象的函数解析式是（ ）
| π |
| 4 |
| π |
| 4 |
A、y=sin（2x+
| ||
B、y=sin（2x+
| ||
C、y=sin（2x-
| ||
| D、y=sin2x |