题目内容
10.椭圆$\frac{x^2}{{4{a^2}}}+\frac{y^2}{{3{a^2}}}=1$(a>0)的左焦点为F,直线x=m与椭圆相交于点A、B,则△FAB的周长的最大值是8a.分析 设椭圆的右焦点为M,则△FAB的周长AF+FB+AB≤FA+AM+FB+BM=8a即可.
解答 解:如图,设椭圆的右焦点为M,由椭圆的方程得椭圆的长轴为2×2a=4a,
△FAB的周长AF+FB+AB≤FA+AM+FB+BM=2×2a+2×2a=8a,
故答案为:8a
点评 本题考查了椭圆的方程、性质、焦点三角形,属于中档题.

练习册系列答案
相关题目
1.在等比数列{an}中,已知a4=8a1,且a1,a2+1,a3成等差数列.则{an}的前5项和为( )
| A. | 31 | B. | 62 | C. | 64 | D. | 128 |
19.若函数$f(x)=\left\{\begin{array}{l}{a^x},x>1\\(4-\frac{a}{2})x+2,x≤1\end{array}\right.$在(-∞,+∞)上单调递增,则的取值范围是( )
| A. | [4,8) | B. | (1,+∞) | C. | (4,8) | D. | (1,8) |
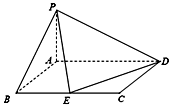 如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.