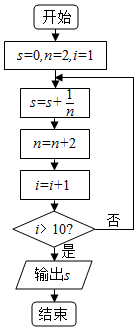
题目内容
6.已知命题p:x2+2x-3>0;命题q:3-x>1,若“(¬p)∧q”为真,则x的取值范围是[-3,1].分析 分别求出关于p,q为真时的x的范围,从而求出复合命题中x的范围即可.
解答 解:关于命题p:解x2+2x-3>0,得:x>1或x<-3,
关于命题q:解3-x>1得:x<2,
若“(¬p)∧q”为真,则p假q真,
∴$\left\{\begin{array}{l}{-3≤x≤1}\\{x<2}\end{array}\right.$,解得:-3≤x≤1,
故答案为:[-3,1].
点评 本题考查了解不等式问题,考查复合命题的判断,是一道基础题.

练习册系列答案
相关题目
17.已知函数f(x)=xn的图象过点(3,$\sqrt{3}$),则n=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
18.下列函数在定义域上不是连续函数的是( )
| A. | f(x)=x2 | B. | f(x)=x | C. | f(x)=$\sqrt{x}$ | D. | f(x)=$\frac{1}{x}$ |
15.已知函数y=f(x)满足f(1)=2,f′(1)=-1,则曲线g(x)=exf(x)在x=1处的切线斜率是( )
| A. | -e | B. | e | C. | 2e | D. | 3e |
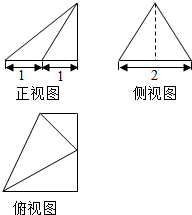 某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.
某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.